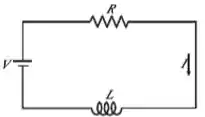
O diagrama esquemático apresentado representa um circuito elétrico que consiste em uma força eletromotriz que produz uma voltagem , um resistor com resistência e um indutor com indutância . A teoria dos circuitos elétricos mostra que, se uma voltagem for aplicada no instante , então a corrente que percorre o circuito no instante é dada por

Qual é o efeito sobre a corrente em um dado tempo fixo, se a resistência tender a zero (isto é, )?

Sendo constante, passamos ela pra fora do limite, e teremos:

Aplicando em , dentro da função, chegaríamos a indeterminação . Podemos resolver isso aplicando a rega de L’Hôpital, derivando numerador e denominador. Vamos ter:

Já podemos aplicar o na função resultante sem problemas. Nisso, vamos obter:

Assim, no que a resistência do circuito tende a ficar cada vez mais próxima de zero, a corrente tende a assumir o valor de .