Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 2

Os problemas de 1 a 6 envolvem equações da forma d y / d t = f y . Em cada problema, esboce o gráfico de f ( y ) em função de y , determine os pontos críticos (de equilíbrio) e classifique cada um como assintoticamente estável ou instável. Desenhe a reta de fase e esboce diversos gráficos de soluções no plano t y

Passo 1

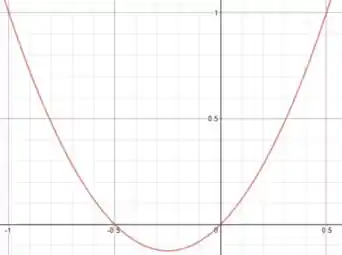
2- Primeiro, fazemos o gráfico da função f ( y ) , que é:

d y / d t = a y + b y 2

Onde a ,   b > 0 e a população inicial está no intervalo - ∞ < y 0 < ∞ . Vamos considerar a = 1 e b = 2 para podermos esboçar o gráfico:

Passo 2

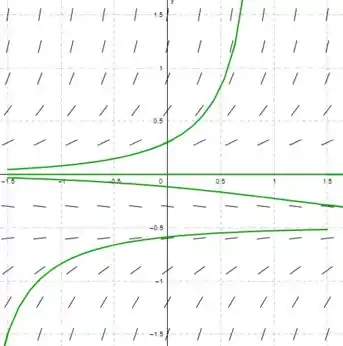
Para fazermos a reta de fase, vamos precisar dos gráficos das soluções:

Passo 3

Podemos ver que algumas soluções crescem com concavidade voltada para cima, outras crescem com concavidade voltada para baixo e também decrescem quase que linearmente, além disso temos uma reta em y = 0 . Assim, nossa reta de fase vai ter a seguinte cara:

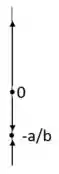
Os pontos y = 0 e y = - a / b serão os pontos de equilíbrio da função, como dá para ver, as soluções em torno de y = 0 ‘divergem’ dessa solução então ela será assintoticamente instável, enquanto as soluções em torno de y = - a / b ‘convergem’ o que significa que ela será estável. Mais formalmente, y ' > 0 quando y > 0 ou y < - a / b , e y ' < 0 quando - a / b < y < 0 .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pessoa P, partindo da origem, move-se na direção positiva do eixo x, puxando um peso ao longo da curva C (chamada tratriz), como mostrado na figura 1.24. O peso, inicialmente localizado no eixo y
Uma curva C no plano reflete os raios de luz de tal modo que todo raio L paralelo ao eixo y é refletido para um único ponto 0. Determine a equação diferencial para a função y = f ( x ) que descreve a
Determine as equações do movimento se o projétil no Problema 12 encontrar uma força de retardamento k (de magnitude k ) agindo tangencialmente à trajetória mas, oposta ao movimento. Veja a Figura 1.21
No Problema 21, suponha que a quantidade de material esquecida é proporcional à quantidade memorizada no instante t . Qual é a equação diferencial para A quando o esquecimento é levado em conta?
Em teoria de aprendizagem, a taxa à qual um assunto é memorizado é proporcional à quantidade ainda a ser memorizada. Se M denota a quantidade total a ser memorizada e A ( t ) a quantidade memorizada n