Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 39
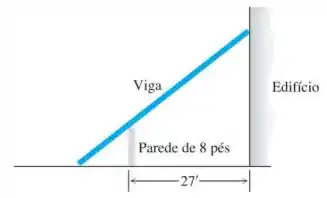
Viga mais curta. O muro de 8 pés mostrado na figura a seguir está a 27 pés do edifício. Determine o comprimento da viga mais curta que alcançará o edifício, apoiado no solo do lado de fora do muro.
Passo 1
Inicialmente, se representarmos essa situação geometricamente, teremos algo desse tipo, galera:
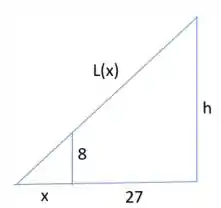
No qual é exatamente o tamanho mínimo da viga que queremos descobrir. É nítido que temos um triângulo retângulo, certo? Dessa forma, podemos utilizar semelhança de triângulo para determinar , se liga:
Isolando , teremos:
Passo 2
Para descobrirmos , podemos utilizar o teorema de Pitágoras, não é mesmo? Dessa forma, teremos:
Substituindo o que descobrimos:
Para descobrirmos o tamanho MÍNIMO da viga, devemos utilizar o conceito de máximos e mínimos, galera! Esse conceito nos diz que temos que derivar a função em questão e igualar a mesma a zero. Se fizermos isso, teremos:
Aqui vale ressaltar que derivamos utilizando a regra da cadeia, tudo bem? Caso não esteja claro, dê uma relembrada lá nas seções anteriores sobre técnicas de derivação, beleza? Continuando, teremos:
Fazendo a distributiva e simplificando:
Passo 3
Agora que chegamos em uma expressão em forma de produto, fica mais tranquilo de resolvermos, não é mesmo? Para o produto que encontramos no passo anterior dar zero, galera, ou (o que não é possível para nós) ou:
Agora que descobrimos o valor de que minimiza o tamanho da viga, basta substituirmos lá na expressão original para descobrirmos, de fato, quanto será o tamanho da mesma, se liga: