Qual é a distância vertical máxima entre a reta e a parábola para ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a máxima distância vertical entre a reta e a parábola , no intervalo . Para visualizar melhor o que ele quer dizer, vamos esboçar o gráfico das curvas e observar um ponto qualquer:
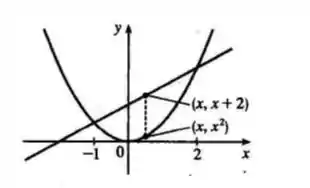
Essa distância vertical será uma função , que nós podemos chamar de . Dessa forma, a distância entre a reta e a parábola será dada por:
Mas a gente quer que essa distância seja máxima, então precisamos calcular a derivada dessa função e igualar o resultado a zero, para encontrar seu ponto de máximo, através do teste da primeira derivada.
Vamos lá!
Passo 2
Como queremos a maior distância entre as curvas, vamos começar derivando nossa função :
Agora igualando esse resultado a zero:
E isolando , temos:
Esse é o único ponto crítico da função. Então, vamos verificar se este ponto é um ponto de máximo no intervalo dado. Pra isso, vamos atribuir alguns valores a , olha só:
Como a função cresce antes de e decresce depois dele, temos que é de fato um ponto de máximo. Portanto, a distância vertical máxima entre as curvas é dada por .
Valeu, galera! Até a próxima! 😉