Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 15b
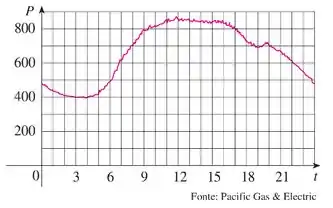
O gráfico mostra o consumo de energia por um dia em setembro em São Francisco. ( é medido em megawatts; é medido em horas a partir da meia-noite).
Quando houve o menor consumo de energia? E quando foi o maior? Esses horários parecem razoáveis?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico do consumo de energia em uma cidade, medido em relação ao tempo , e pediu pra gente verifica quando houve o menor e o maior consumo de energia e se esses horários parecem razoáveis.
Pra isso, precisamos prestar atenção em como se comporta a nossa curva no intervalo de tempo considerado. Então, vamos verificar os valores da potência nos pontos de mínimo e máximo da curva e analisar os resultados.
Vamos lá!
Passo 2
Vamos traçar uma reta em torno do menor ponto de da curva e analisar o horário correspondente:
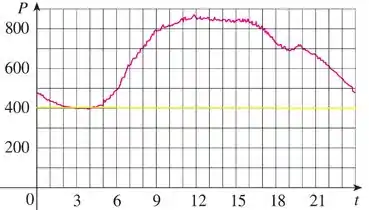
Olhando bem pro gráfico, percebemos que o menor consumo de energia é as :
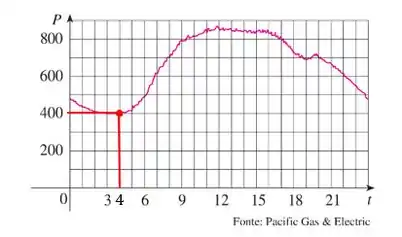
O consumo mínimo às da manhã é razoável, já que é o horário que normalmente as pessoas desligam luzes e aparelhos em geral para dormirem.
Além disso, a indústrias (que consomem bastante energia elétrica) estão fechadas.
Passo 3
Agora vamos fazer a mesma coisa para o maior valor:
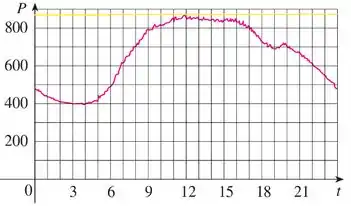
Observe que o maior consumo é por volta das :
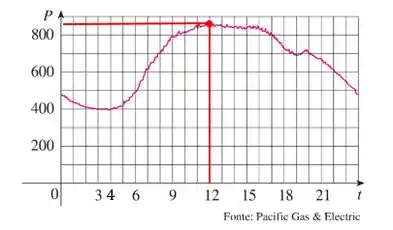
Essa valor também é razoável para um maior consumo de energia, já que é o horário em que as pessoas estão acordadas, geralmente almoçando ou preparando refeições e usando mais aparelhos eletrodomésticos.
Além disso, a indústria e o coJmércio estão em horário de pleno funcionamento, o que colabora no aumento do consumo.
Entendeu direitinho?? Responde aí! 😉