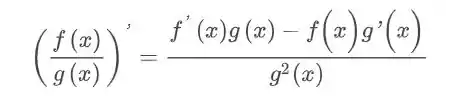Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 4.5 - Ex. 14

14. z = (x^2 - y^2)/(x^2 + y^2)

Passo 1

Derivada de Polinômio

A brincadeira agora é saber a derivada de um polinômio qualquer  x^n . Bem, o resultado dessa brincadeira é:

f^' (x) = n x^(n - 1)

Basta multiplicar o polinômio por  n  e subtrair  1  no  n  do expoente de  x .

Derivada de constante

A brincadeira agora é saber a derivada de uma constante qualquer  x n . Bem, o resultado dessa brincadeira é:

f (x) = x n

f^' (x) = n

Passo 2

Vamos aplicar a regra do quociente:

Passo 3

f ( z ) = (x^2 - y^2)/(x^2 + y^2)

(del z)/(del x) = ((x^2 + y^2) * (2 x - 0) - (x^2 - y^2) * ( 2 x + 0 ))/((x^2 + y^2)^2)

= (2 x^3 + 2 x y^2 - 2 x^3 + 2 x y^2)/((x^2 + y^2)^2)

= (4 x y^2)/((x^2 + y^2)^2)

Passo 4

f ( z ) = (x^2 - y^2)/(x^2 + y^2)

(del z)/(del y) = ((x^2 + y^2) * (0 - 2 y) - (x^2 - y^2) * ( 0 + 2 y ))/((x^2 + y^2)^2)

= (- 2 x^2 y - 2 y^3 - 2 y x^2 + 2 y^3)/((x^2 + y^2)^2)

= - (4 x^2 y)/((x^2 + y^2)^2)

Resposta

(del z)/(del x) = (4 x y^2)/((x^2 + y^2)^2)

(del z)/(del y) = - (4 x^2 y)/((x^2 + y^2)^2)

Ver Outros Exercícios desse livro