Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 11
Dois carros iniciam o movimento de um mesmo ponto. Um viaja para o sul a 60 mi/h, e o outro para o oeste a 25 mi/h. A que taxa está crescendo a distância entre os carros duas horas depois?
Passo 1
Opa, bora lá! Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que tem dois carrinhos que saem no mesmo momento e de um mesmo ponto, mas um segue pro sul e o outro pro oeste, cada um com a sua velocidade. Depois de nos falar isso, ele nos pede a variação da distância entre eles depois de duas horas da partida.
Vamos fazer um esqueminha pra entender o que tá acontecendo.
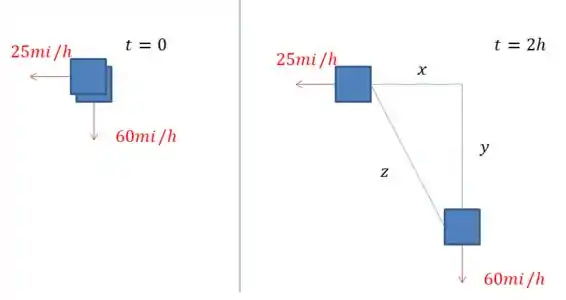
Queremos encontrar aqui a variação da distância entre eles, isso é:
Sabemos que a distância entre eles é a hipotenusa de um triângulo, logo:
E podemos perceber que a velocidade do carro que vai para Oeste é a taxa de variação da coordenada , isso é:
E o mesmo pode-se dizer sobre o carro que vai para o Sul, só que esse é a variação da coordenada .
Para encontrar vamos derivar a expressão que vêm da regra de Pitágoras.
Viu, nem é tão difícil assim. Eaii, partiu??
Passo 2
Já vimos que é um triângulo retângulo, então nos resta aplicar Pitagoras.
E derivar ambos os lados com relação ao tempo.
Podemos dividir ambos os lados por , assim, teremos:
Agora basta encontrarmos os valores de e. Sabemos que estamos no tempo , e nos foi dado as velocidades em e em , logo:
E para encontrar , vamos usar a expressão de Pitágoras.
E como é uma distância positiva, temos:
Passo 3
Agora basta substituir tudo na expressão que encontramos quando derivamos:
Prontinho!!