Uma escada de 8m está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé́ da parede a uma velocidade constante de 2 (m/s), com que velocidade a extremidade superior estará́ descendo no instante em que a inferior estiver a 3m da parede?

Essa variação, ocorre a uma taxa de - 6 55 (m/s).

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.15 - Ex. 16

Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé́ da parede a uma velocidade constante de (m/s), com que velocidade a extremidade superior estará́ descendo no instante em que a inferior estiver a da parede?

Passo 1

Podemos ver que a escada descreve um triangulo retângulo com a parede e o chão.

Podemos ilustrar a situação da seguinte maneira, vamos chamar de , a altura da ponta da escada encostada na parede, e de , a distância do pé da escada à parede:

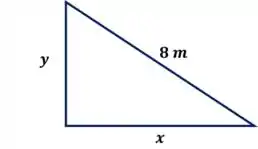
Assim, a relação entre e pode ser dada por Pitágoras:

Passo 2

Derivando toda a relação em função do tempo, temos:

Passo 3

Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de (m/s), o valor de estará variando à taxa de . Então, no momento em que a parte inferior estiver a da parede, ou seja, , temos que:

Assim, se , e , temos que

O valor negativo, nos certifica que está decrescendo, ou seja, a extremidade superior estará descendo. Assim, essa variação, ocorre a uma taxa de (m/s).

Resposta

Essa variação, ocorre a uma taxa de (m/s).

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de uma partícula que se desloca ao longo de eixo x depende do tempo de acordo com a equação x = - t 3 + 3 t 2 , t ≥ 0 .a) Estude o sinal de v t .b) Estude o sinal de a t .c) Calcule lim t →

Seja x = f t ,t ≥ 0 ,t a lq u e f 0 = 1 e f 1 = 2 . Suponha, ainda, que d x d t0 para t ≥ 0 ; d 2 x d t 20 para 0t1 e d 2 x d t 20 para t1 . Como você acha que deve ser o gráfico de f ? Porquê?

Enche-se um reservatório, cuja forma é a de um cone circular reto, de água a uma taxa de 0,1 m³/s. O vértice está a 15 m do topo e o raio do topo é de 10 m. Com que velocidade o nível h da água e

Dois pontos P e Q deslocam-se, respectivamente, nos eixos x e y de modo que a soma das distâncias de P a R e de R a Q mantém-se constante e igual a e durante o movimento, em que R = 0 , h é um ponto