Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 41

Dois lados de um triângulo têm comprimento de 12 m e 15 m. O ângulo entre eles aumenta à taxa de 2 ° / m i n . Com que velocidade estará aumentando o terceiro lado quando o ângulo dos lados de comprimento fixo estiver em 60°?

Passo 1

Opa, bora resolver esse problema!

Temos um triângulo com dois lados de comprimento 12   m e 15   m e o ângulo entre eles aumenta à taxa de 2 ° / m i n . Dito isso o enunciado pede pra a gente calcular com que velocidade estará aumentando o terceiro lado quando o ângulo dos lados de comprimento fixo estiver em 60°.

Bora fazer um desenho pra ajudar a compreensão. Se chamarmos de θ , o ângulo entre os lados fixos e x o comprimento do terceiro lado. Temos:

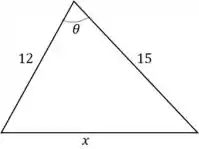
O que temos aqui é:

d θ d t = 2 ° / m i n

E o que queremos é :

d x d t

Agora vamos relacionar esses dois carinhas!

Passo 2

Temos dois lados fixos e queremos relacionar o ângulo entre eles com o lado oposto a ele, então podemos usar a lei dos cossenos:

x 2 = 12 2 + 15 2 - 2 × 12 × 15 × cos ⁡ θ

x 2 = 369 - 360 cos ⁡ θ

Passo 3

Agora devemos derivar a equação em função do tempo t em minutos, usando derivada implícita, para obter a relação entre suas taxas:

2 x d x d t = - 360 ( - sen ⁡ θ ) d θ d t

d x d t = 180 sen ⁡ θ d θ d t x

Se x 2 = 369 - 360 cos ⁡ θ então x = 369 - 360 cos ⁡ θ , logo:

d x d t = 180 sen ⁡ θ × θ ' t 369 - 360 cos ⁡ θ

Passo 4

Devemos lembrar de converter sempre graus para radianos.

Se no momento em que θ = 60 ° = π / 3 , θ ' t = 2 ° / m i n = π 90 r a d / m i n e portanto:

d x d t = 180 sen ⁡ π 3 × π 90 369 - 360 cos ⁡ π 3

d x d t = π 7 21 = 0,3958034706

Logo, o comprimento do terceiro lado está variando a aproximadamente 0,4   m / m i n .

Resposta

O comprimento do terceiro lado está variando a aproximadamente 0,4   m / m i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula desloca-se sobre o eixo x com função de posição x = 1 2 t + 1 , t ≥ 0 .a) Qual a velocidade no instante t ?b) Qual a aceleração no instante t ?c) Esboce o gráfico da função de posição.
Um ponto P move-se sobre a parábola y 2 = x , x0 e y0 . A abscissa x está variando com uma aceleração que, em cada instante, é o dobro do quadrado da velocidade da ordenada y . Mostre que a ordena
O ponto P = x ,y está fixo à roda de raio 1 m, que rola, sem escorregamento, sobre o eixo x . O ângulo θ está variando a uma taxa constante de 1 rad/s. Expresse as velocidades da abscissa e da orde
Um ponto P move-se ao longo do gráfico de y = 1 x 2 + 1 de tal modo que a sua abscissa x varia a uma velocidade constante de 5 (m/s). Qual a velocidade de y no instante em que x = 10 m ?
Um ponto move-se sobre a semicircunferência x 2 + y 2 = 5 , y ≥ 0 . Suponha d x d t0 . Determine o ponto da curva em que a velocidade de y seja o dobro da de x .