Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.1 - Ex. 67
Qual dos dois é maior, ou ? As calculadoras diminuíram o mistério dessa questão, que costumava ser desafiadora. (Verifique você mesmo; você vera que, surpreendentemente, eles estão quase empatados.) No entanto, a questão também pode ser respondida sem uma calculadora.
- Determine uma equação para a reta que passa pela origem e é tangente ao gráfico .
- Ofereça um argumento baseado nos gráficos de e da reta tangente para explicar por que para qualquer , positivo ,
- Mostre que para qualquer positivo
- Então, qual dos dois é maior, ou ?
Passo 1
a)
Para acharmos uma reta, precisamos saber o coeficiente angular e um ponto que pertence a ela. Como ela passa pela origem, então o ponto está na reta. Para acharmos o coeficiente angular da reta, vamos pegar a derivada no ponto de interseção da reta com a curva. Se considerarmos o coeficiente angular como :
Logo,
Agora vamos fazer a interseção com a curva
Assim,
Para o coeficiente angular:
Derivando,
No ponto de interseção :
Como :
Portanto,
Para acharmos o coeficiente angular, basta usarmos que :
Então a reta fica o seguinte:
Passo 2
b) Esboçando um gráfico de e , vai ficar assim ó:
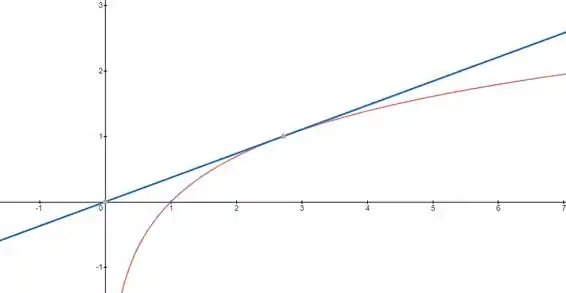
Repare que para todos os valores de positivos diferentes de o da reta é sempre maior que que o da curva . Dessa forma para e :
Assim,
Passo 3
c) Do Passo anterior, sabemos o seguinte:
Isto é,
Lá de logaritmos:
Usando esse lembrete em :
Como :
d) Portanto, teremos que para todos os valores positivos diferentes de :
Passo 4
e) Se fizemos :
Portanto o maior valor será