Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 05d
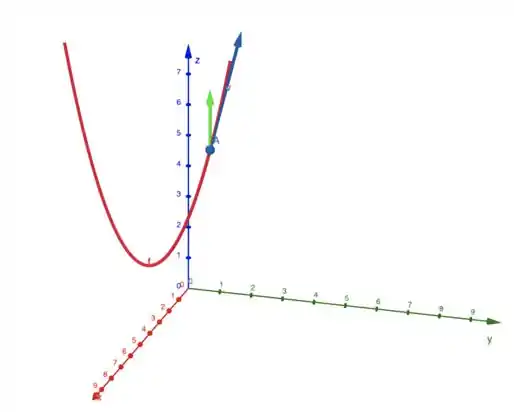
dois vetores tangentes unitários à trajetória de partícula em t = t1. Trace um esboço da trajetória da partícula e represente geometricamente os vetores V(t1) e A(t1).
Passo 1
Dada da função vetorial da posição
e , podemos encontrar a velocidade e aceleração a partir da função vetorial da posição aplicando derivadas. Olha:
Passo 2
Pra encontrar um vetor tangente à trajetória, a gente pode derivar nosso vetor posição fornecido pelo enunciado. Mas repara que a derivada da posição em função do tempo é a própria velocidade. Então, temos que
e aplicado no ponto t1, temos que
Então, o vetor
é um vetor tangente à trajetória. Mas calma!! O enunciado pede vetores que sejam tangentes e unitários… Pra gente fazer um vetor se tornar um vetor unitário, a gente pode dividi-lo pelo seu próprio módulo. Assim:
Mas o enunciado pede dois vetores tangentes unitários… Mas pra gente achar outro, podemos malandramente multiplicar esse por .
Pronto! Agora temos dois vetores tangentes unitários à trajetória. São eles:
Passo 3
Agora bora esboçar a trajetória da partícula. A função vetorial da trajetória é essa aqui:
E se a gente desparametrizar, vai ficar assim:
Então a gente pode concluir que no plano , o movimento da partícula é uma parábola. Além disso, também sabemos que , uma constante. Então, nosso esboço fica assim:
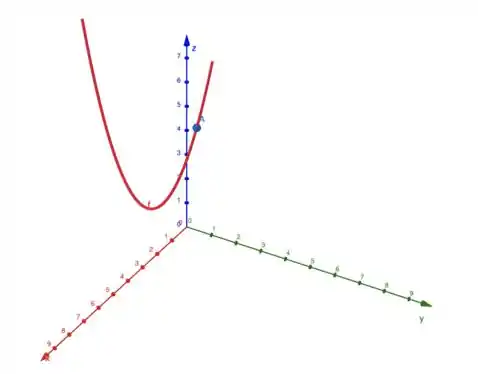
Agora só falta a gente representar geometricamente os vetores e nesse esboço. A partícula tá sendo representada pelo objeto ali!
Passo 4
Aplicando as funções vetoriais da velocidade e da aceleração em :
E juntando-os ao nosso lindo esboço, fica assim
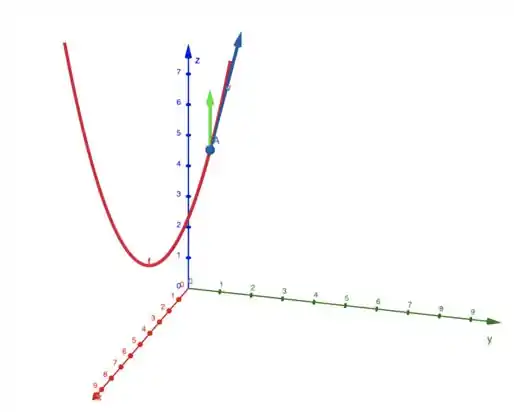
Onde a seta verde e a azul representam, respectivamente, os vetores e .
Resposta
e
