Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4m
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vou ajudar vocês nessa questão. Bora lá?
Para esboçar o domínio precisamos pensar se essa função “falha” para algum valor de . Mas como assim?
Bom, sabemos de duas grandes “falhas” da matemáticas:
Divisão por zero
Raiz (de índice par) negativa.
Daí para dar o domínio da função basta identificar se alguma dessas situações pode acontecer na função que temos.
Como a função que temos é a função módulo, que é “quebrada”, devemos identificar nas duas partes dela se há alguma indeterminação matemática.
Passo 2
Como relembrar é viver, vamos revisar as propriedades da função modular?
Sendo a função modular , ela é definida da seguinte forma:
Ela tem duas caras: uma antes de zero e outra depois. Mas quanto ao domínio, é tranquilo da gente entender. Em nenhuma das duas partes identificamos alguma inconsistência matemática, sendo assim o domínio é o mais abrangente possível, o conjunto dos reais. Assim:
Agora vamos aplicar isso para a nossa função?
Passo 3
A função que o problema dá é essa aqui:
E pode ser definida da seguinte forma:
Pra analisar o domínio devemos ver se as duas partes da função (antes do zero e depois) apresentam alguma indeterminação. Bom, como é um polinômio de primeiro grau, então não temos algum valor de no qual a função falha! Beleza! Assim sabemos que o domínio dela são todos os reais:
Certo! Vamos passar para o gráfico?
Passo 4
Vamos primeiro ver onde a função corta o eixo dos :
Assim:
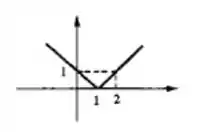
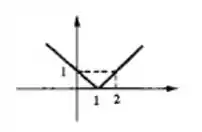
Beleza! Então o ponto pertence ao gráfico e é justamente onde as retas e se encontram!
E agora onde corta o eixo ? Onde temos:
Então a função (reta crescente) corta o eixo no ponto .
Agora pra completar tudo, vamos determinar um ponto depois de que pertence a outra parte da função na parte positiva. Digamos (usando a parte positiva da função):
Encontramos o ponto ! Beleza! Agora o próximo passo é colocar tudo isso num gráfico! Bora lá?
Passo 5
Então sabemos que para a função é uma reta decrescente, que passa pelos pontos e . E que para valores é uma reta crescente que passa pelos pontos e :
Resposta
