Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4q
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vou ajudar vocês nessa questão. Bora lá?
Para esboçar o domínio precisamos pensar se essa função “falha” para algum valor de . Mas como assim?
Bom, sabemos de duas grandes “falhas” da matemáticas:
Divisão por zero
Raiz (de índice par) negativa.
Daí para dar o domínio da função basta identificar se alguma dessas situações pode acontecer na função que temos.
Dá uma espiada lá na função. Xiiii, temos um no denominador! Aqui atenção! Uma as regras é que o denominador não pode assumir o valor zero. Então o denominador deve ser :
Logo temos que a função falha quando temos . Mas e em outros lugares? Outros lugares não temos indeterminação, portanto ela pode assumir todos os outros valores de =)
Com isso o domínio dessa função são quase todos os números reais, A NÃO SER pelo valor , que deve ser retirado!
Assim temos:
Uma outra forma de escrever é:
Passo 2
Como relembrar é viver, vamos revisar as propriedades da função modular?
Sendo a função modular , ela é definida da seguinte forma:
Ela tem duas caras: uma antes de zero e outra depois.
Assim a função de até zero vai ser:
E de zero até vale:
Mas aqui atenção!! A bolinha em deve ser aberta, pois ali a função não está definida!!
Então daqui tiramos que a função assume o valor de até o zero e depois “pula” para . Vamos ver como fica no gráfico?
Passo 3
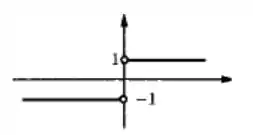
Colocando as informações que a gente viu no passo anterior num gráfico temos:
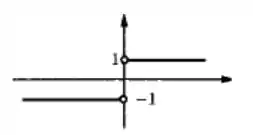
Viram como em o gráfico tem um “salto”? E notaram também a bolinha aberta nos dois pontos?
Beleza! Era isso pessoal, até a próxima!
Resposta
