Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4r
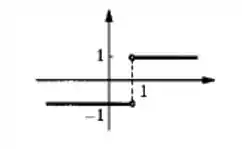
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vamos começar essa questão achando o domínio!
Para esboçar o domínio precisamos pensar se essa função tem alguma restrição para o valor de . Entre as restrições temos:
- O denominador em uma fração não pode ser zero
- O argumento de uma raiz par não pode ser menor que zero
- O argumento de uma função logarítmica não pode ser negativo
Dá uma espiada lá na função. Xiiii, temos um no denominador! Aqui atenção! Uma as regras é que o denominador não pode assumir o valor zero. Então o denominador deve ser :
Com isso o domínio dessa função são quase todos os números reais, A NÃO SER pelo valor , que deve ser retirado!
Assim temos:
Uma outra forma de escrever é:
Agora vamos para o gráfico!
Passo 2
Como relembrar é viver, vamos revisar as propriedades da função modular?
Sendo a função modular , ela é definida da seguinte forma:
Ela tem duas caras: uma antes de zero e outra depois.
Assim a função de até (que é onde ela muda de “cara”) vai ser:
E de 1 até vale:
Mas aqui atenção!! A bolinha em deve ser aberta, pois ali a função não está definida!!
Então daqui tiramos que a função assume o valor de até o zero e depois “pula” para . Vamos ver como fica no gráfico?
Passo 3
Colocando as informações que a gente viu no passo anterior num gráfico temos:
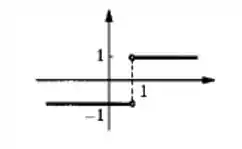
Certo pessoal?
Até a próxima =)
Resposta
