Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4a
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vou ajudar vocês nessa questão. Bora lá?
Para esboçar o domínio precisamos pensar se essa função “falha” para algum valor de . Mas como assim?
Bom, sabemos de duas grandes “falhas” da matemáticas:
- Divisão por zero
- Raiz (de índice par) negativa.
Daí para dar o domínio da função basta identificar se alguma dessas situações pode acontecer na função que temos.
Passo 2
Temos aqui um polinômio de grau um. Então descartamos logo as duas situações problemáticas, não é? Beleza! Então o domínio de são todos os elementos pertencentes ao conjunto dos números reais, o mais abrangente de todos =D
Assim:
Passo 3
Agora vamos desenhar o gráfico. Primeiro vamos determinar os pontos onde a função corta os eixos cartesianos:
- No eixo : Então corta no ponto
- No eixo : Então no ponto
Xiii, deu o mesmo ponto. E agora? Bom, para esboçar uma reta precisamos de pelo menos dois pontos. Então vou chutar um valor de , por exemplo . E agora substituir na função para determinar a ordenada correspondente:
Certo! Agora temos dois pontos: a origem e o ponto . Agora é só colocar no gráfico:
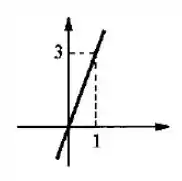
Resposta
