Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.10 - Ex. 29b

Drenagem de um reservatório hemisférico Agua escoa a uma taxa de 6 m 3 /min de um reservatório hemisférico com raio de 13 m, mostrado aqui em perfil.

Responda às questões a seguir, sendo o volume de água em um recipiente hemisférico de raio R dado por V = π 3 y 2 ( 3 R - y ) , quando a água tiver y metros de profundidade.

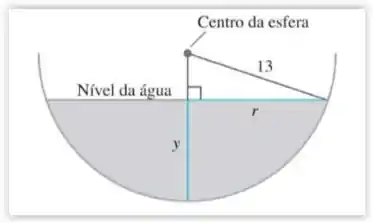
a. Qual será a taxa de variação do nível da água quando a profundidade for de 8 m?

b. Qual será o raio r na superfície da água quando ela tiver y metros de profundidade?

c. Qual será a taxa de variação do raio r quando a profundidade da água for de 8 m?

Passo 1

Da figura conseguimos ver um triângulo retângulo formada pelo cateto r e pela hipotenusa 13.

Desses valores conseguimos tirar o valor do outro cateto(x) que terá valor igual a:

x =   169 - r 2

Passo 2

Esse cateto que acabamos de encontrar somado com o nível de profundidade da água y terão o mesmo valor que o raio R da esfera.

R = x + y

Resultando em :

13 = 169 - r 2 + y

Passando o y pro outro lado temos :

13 - y = 169 - r 2

Passo 3

Agora elevando ao quadrado os dois lados temos:

169 - 26 y + y 2 = 169 - r 2

Resultando em:

- 26 y + y 2 = - r 2

Resposta

Multiplicando por -1 os dois lados e tirando a raiz, temos:

r = 26 y - y 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Café está sendo derramado a uma taxa uniforme de 20c m 3 / s em uma xícara em forma de cone truncado (ver figura abaixo). Se os raios superior e inferior da xícara forem de 4 e 2c m e a altura for de
Uma partícula move-se ao longo da curva 16 x 2+9 y 2=144 . Encontre todos os pontos ( x ,y ) nos quais as taxas de variação de x e de y em relação ao tempo são iguais. [Suponha que d x / d t e d y / d
Em um relógio, o ponteiro dos minutos tem 4c m de comprimento e o das horas, 3c m . Com que rapidez estará variando a distância entre as extremidades do ponteiro às 9h o r a s ?
Um ponto P está movendo-se ao longo de uma reta cuja equação é y=2 x . Com que rapidez estará variando a distância entre P e o ponto ( 3 ,0 ) no instante em que P estiver em ( 3 ,6 ) se x estiver decr
Um helicóptero está voando em direção ao norte a 100k m / h e a uma altitude constante de 0,5k m . Abaixo, um carro viaja para o oeste em uma estrada a 75k m / h . No momento em que o helicóptero cruz