Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.4 - Ex. 8b

Duas espécies de peixe que competem por comida, mas não caçam um ao outro, são o lepomis macrochirus, um peixe de água fresca e cor azulada que habita águas norte-americanas, que chamaremos de peixe azulado, e lepomis microlofus, um peixe do sudeste e centro dos Estados Unidos com guelra vermelha brilhante que chamaremos de vermelhão. Suponha que um lago está cheio desses dois tipos de peixes e denote por x e y, respectivamente, as populações de peixe azulado e de vermelhão no instante t. Suponha, ainda, que a competição é modelada pelas equações:

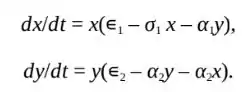
Se ∊1/σ1 > ∊2/α2 e ∊1/α1 > ∊2/σ2, mostre que as únicas populações de equilíbrio no lago são: sem as duas espécies, sem o vermelhão ou sem o peixe azulado. O que vai acontecer para valores grandes de t?

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos os valores críticos das equações e achar o equilíbrio. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser determinar quais os pontos críticos, ou seja, igualar as derivadas a zero.

x ϵ 1 - σ 1 x - α 1 y = 0

y ϵ 2 -   σ 2 y - α 2 x = 0

Igualando o x a zero na segunda equação e o y a zero na primeira, temos os seguintes pontos críticos:

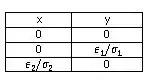
Passo 3

Pronto!! Agora é só acharmos o ponto que seja assinttoticamente estável.

Vou te deixar montar pros 3 aí, mas já vou botar aqui o certo, ok??

ϵ 1 - α 1 ϵ 2 σ 2 - λ 0 - α 2 ϵ 2 σ 2 - ϵ 2 - λ = 0

λ 1 =   - ϵ 1 < 0

λ 2 = ϵ 2 σ 1 - α 2 ϵ 1 σ 1

Assim, com t → ∞ , x → ϵ 1 σ 1 e y → 0

Resposta

Assim, com t → ∞ , x → ϵ 1 σ 1 e y → 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neste problema, vamos mostrar como pequenas mudanças nos coeficientes de um sistema de equações lineares podem afetar um ponto crítico que é um centro. Considere o sistema x ' = 0 1 - 1 0 x Mostre que
Neste problema, vamos deduzir uma fórmula para o período natural de um pêndulo não linear não amortecido [ c=0 na Eq. (10) da Seção 9.2]. Suponha que a massa é puxada por um ângulo positivo α e depois
30. Uma generalização da equação do pêndulo amortecido discutida no texto, ou de um sistema mola-massa amortecido, é a equação de Liénard d 2 x d t 2 + c x d x d t + g x = 0 Se c ( x ) for uma constan
23. O movimento de determinado pêndulo não amortecido é descrito pelas equações d x d t = y ,d y d t = - 4 sin ⁡ x Se o pêndulo for colocado em movimento com um deslocamento angular A e sem velocidade
Considere o sistema (2) no texto e suponha que σ1σ2 – α1α2 = 0.Encontre todos os pontos críticos do sistema. Observe que o resultado depende se σ1∊2 –α2∊1 é nulo ou não.