Encontre os pontos na curva onde a reta tangente é horizontal ou vertical. Se você tiver uma ferramenta gráfica, trace a curva.
Passo 1
Olá, meu amigooo. A gente tem aqui a curva com parametrização:
E a gente tem que encontrar pontos onde uma reta tangente a essa curva é horizontal ou vertical.
A reta tangente é horizontal quando
E vertical quando
Então, vamos achar essas derivadas, igualas a zero para encontrar os valores de em que isso ocorre e depois substituir na parametrização da curva para encontrar os pontos correspondentes.
Passo 2
Vamos começar por quando a reta tangente é horizontal.
Vamos então aplicar a derivada e então igualar a zero:
Temos que o cosseno nesse valor é o de:
Então o valor de :
Passo 3
Substituindo na parametrização da curva para encontramos o valor dos pontos, temos:
Portanto, a reta tangente é horizontal no ponto
Passo 4
Agora vamos descobrir quando a reta tangente é vertical.
Derivando e igualando a zero:
Temos então que :
Passo 5
Substituindo na parametrização da curva, temos:
Portanto, a reta tangente é vertical no ponto
Passo 6
Bom, vamos plotar essa curva só pra você ver como é a cara doidinha dela e tentar imaginar as retas tangentes nos pontos que a gente achou aí na questão:
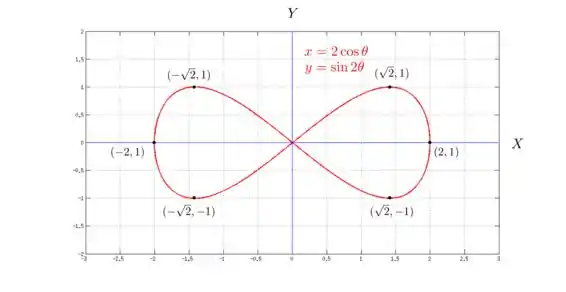
Resposta
A reta tangente é horizontal no ponto
E vertical no ponto