Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 18

Encontre uma equação da elipse. A seguir localize seus focos.

Passo 1

Fala pessoal! Tranquilo? Vamos começar com algumas sugestões do que podemos fazer para encontrar a equação da elipse e os seus focos

  1. Analisar os pontos do gráfico e comparar com a equação da elipse.

    2. ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1

  2. Encontrar o foco pela equação

f = ( h ± a 2 - b 2 , k )

Onde ( h , k ) são as coordenadas do centro da elipse.

Eai? Vamos começar?

Passo 2

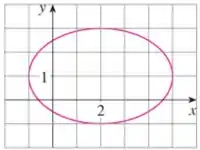
Nessa questão, nos foi dada um gráfico de elipse para determinarmos sua equação e focos.

Na letra A , começamos observando a imagem e identificando os seguintes temos: o semieixo maior ( a = 3 ) , o semieixo menor b = 1 e o centro da elipse ( h , k ) = ( 2,1 )

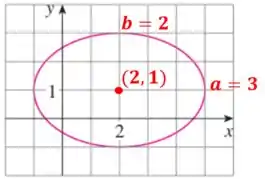
Como a equação geral de uma elipse é dada por

( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1

Podemos substituir os valores tirados do gráfico, então ficamos com:

( x - 2 ) 2 9 + ( y - 1 ) 2 4 = 1

Passo 3

Na letra b , temos que calcular o foco de uma elipse desse tipo é dado por

f = h ± a 2 - b 2 , k

Temos que o ponto ( h , k ) = ( 2,1 ) , local do centro da elipse, e a = 3 é o semieixo maior e b = 2 é o semieixo menor.

f = 1 ± 3 2 - 2 2 , 1

Resolvendo

f = 2 ± 9 - 4 , 1

então, f = ( 2 ± 5   , 1 )

Resposta

( x - 2 ) 2 9 + ( y - 1 ) 2 4 = 1

f = ( 2   ± 5   , 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando a equação cartesiana para
Os Exercícios 1-6 fornecem equações paramétricas e intervalos paramétricos para o movimento de uma partícula no plano x y . Identifique a trajetória da partícula encontrando uma equação cartesiana par