Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 4

Encontrando um centroide: encontre o centroide da região no primeiro quadrante delimitado pelas reta x + y = 3

Passo 1

Faaaala, cara! Tranquileba?

Temos de cara pela equação dada que (podemos fazer uma dependência):

x = 3 - y

e com dependência no y, logo:

x ∈ 0,3   e   y ∈ 0,3 - x

E temos que:

x c e n t = ∬ y   d x d y M

E análogo para y c e n t

y c e n t = ∬ x   d x d y M

E para M:

M = ∬ d x d y

Passo 2

Assim, para M:

M = ∫ 0 3 ∫ 0 3 - x d y d x

∫ 0 3 ( y 0 3 - x   d x

∫ 0 3 3 - x d x

3 x 0 3 - 1 2 x 2 0 3

M = 9 2

Passo 3

E para M y :

M y = ∫ 0 3 ∫ 0 3 - x x   d y   d x

∫ 0 3 x y 0 3 - x   d x

∫ 0 3 x 3 - x d x

3 2 x 2 0 3 - 1 3 x 3 0 3

M y = 9 2

E para M x :

M x = ∫ 0 3 ∫ 0 3 - x y   d y d x

∫ 0 3 1 2 y 2 0 3 - x d x

∫ 0 3 1 2 9 - 6 x + x 2 d x

9 2 x 0 3 - 3 2 x 2 0 3 + 1 6 x 3 0 3

M x = 9 2

Veja que M y = M _ x o que já era visível por simetria:

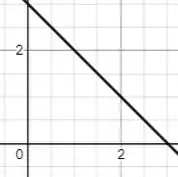
E como já dito anteriormente:

x c e n t = M y M

y c e n t = M x M

Logo

x c e n t = y c e n t = 1

E visível por simetria.

Resposta

x c e n t = y c e n t = 1

E visível por simetria.

Exercícios de Livros Relacionados

Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Encontre o centro de massa do sólido E com a dada função de densidade ρ .
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O sólido do exercício 19; ρ x , y , z = x 2 + y 2
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.O hemisfério x 2 + y 2 + z 2 ≤ 1 ,z ≥ 0 ; ρ x , y , z = x 2
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a 4 k g m 3 . z = x 2 + y 2 z = 9 - x 2 - y 2