Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 1

Encontrando um centro de massa: Encontre o centro de massa de uma placa fina de densidade δ = 3 delimitada pelas retas x = 0 , y = x e a parábola y = 2 - x 2 no primeiro quadrante.

Passo 1

Faaaala, cara! Tranquileba?

Pela definição do centro de massa, temos:

x   o u   y c m = ∑ i n x   o u   y i * m M

Analisando os gráficos das retas e da parábola:

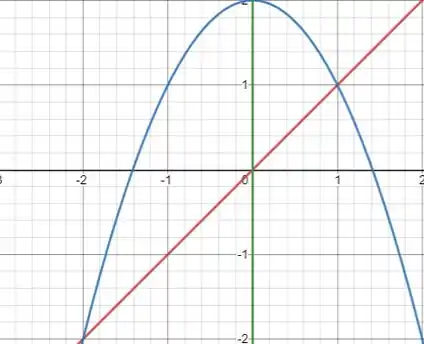
Podemos perceber que 0 ≤ x ≤ 1 e x < y < 2 - x 2

Assim, ficamos com:

M = ∫ 0 1 ∫ x 2 - x 2 δ   d y d x

Passo 2

Primeiro, achemos a massa total, ou ∑ i n m = M

M = δ ∫ 0 1 ∫ x 2 - x 2 d y d x  

M = 3 ∫ 0 1 y x 2 - x 2 d x

M = 3 ∫ 0 1 2 - x 2 - x d x

M = 3 ∫ 0 1 2 d x - ∫ 0 1 x 2 d x - ∫ 0 1 x d x  

M = 3   2 x 0 1 - x 3 3 0 1 - x 2 2 0 1

M = 3 7 6 = 7 2

Passo 3

Assim, para o centro de massa em x:

M x = ∫ 0 1 ∫ x 2 - x 2 3 y   d y   d x =

= 3 ∫ 0 1 y 2 2 x 2 - x 2 d x

3 ∫ 0 1 x 4 - 5 x 2 + 4 2 d x =

3 2 ∫ 0 1 x 4 d x - ∫ 0 1 5 x 2 d x + ∫ 0 1 4 d x =

3 2 x 5 5 0 1 - 5 x 3 3 0 1 + 4 x 0 1

M x = 3 2 38 15 = 19 5

E para M y :

M y = ∫ 0 1 ∫ x 2 - x 2 3 x   d y   d x =

= ∫ 0 1 ∫ x 2 - x 2 3 x   d y   d x

= ∫ 0 1 y x 2 - x 2 3 x d x

= ∫ 0 1 2 - x 2 - x 3 x d x

3 ∫ 0 1 x - x 3 - x 2 d x

3 ∫ 0 1 x   d x - ∫ 0 1 x 3 d x -   ∫ 0 1 x 2 d x

3   x 2 2 0 1 - x 4 4 0 1 - x 3 3 0 1

M y = 3 5 12 = 5 4

Logo pela equação dada anteriormente:

x   o u   y c m = ∑ i n x   o u   y i * m M

Temos:

x c m = 5 4 7 2 = 5 14

E

y c m = = 19 5 7 2 = 38 35

Resposta

x c m = 5 4 7 2 = 5 14

E

y c m = = 19 5 7 2 = 38 35

Exercícios de Livros Relacionados

Calcular a massa e as coordenadas do centro de massa dos sólidos delimitados pelas superfícies dadas, supondo a densidade de massa constante. x 2 + y 2 + z 2 - 2 z
Determinar a massa do sólido acima do plano X Y , delimitado pelo cone 9 x 2 + z 2 = y 2 e o plano y = 9 . A densidade no ponto P ( x , y , z ) é proporcional à distância do ponto ao plano X Y .
Calcular a massa dos sólidos limitados pelas superfícies dadas, considerando a densidade de massa igual a 4 k g / m 3 . z = 4 - x 2 - y 2ez = x 2 + y 2
Verificar que o centro de massa de uma esfera de raio 1 coincide com seu centro, sabendo que a sua distribuição de massa é homogênea.
Calcular a massa e as coordenadas do centro de massa dos sólidos delimitados pelas superfícies dadas, supondo a densidade de massa constante. b )x + y = 2 , z = 2 + y e os planos coordenados.