Encontre a área da região sombreada integrando em relação a x:
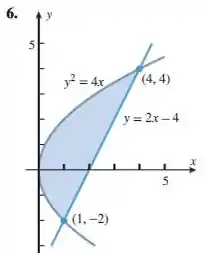
Passo 1
Para calcularmos a área entre as curvas vamos calcular a integral fazendo a diferença entre as funções de cima e debaixo, no entanto, como o enunciado nos pediu para calcularmos em relação a x, observe que dividi em duas regições diferentes (à esquerda e à direita da linha vermelha).
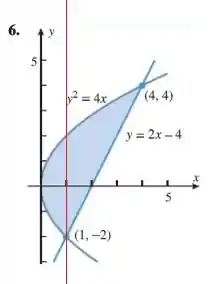
Calculando a área à direita, temos:
Para calcularmos a área a esquerda, observe que a função de cima é a parte positiva da , enquanto a função debaixo é a parte negativa dessa mesma função (). Nossa integral ficará então:
No fim basta somar os resultados!
Passo 2
Calculando a primeira integral temos:
Calculando a segunda integral temos:
Somando os resultados temos: