Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.12 - Ex. 16

Encontrar a derivada das funções dadas. A seguir, comparar os resultados encontrados com os resultados obtidos a partir do uso de um software algébrico.

f t = 2 - t 2 t - 2

Passo 1

Vamos lá, aqui a gente deriva pela Regra do quociente:

f ' t = - 2 t t - 2 - 1 2 - t 2 t - 2 2

f ' t =   - 2 t 2 + 4 t - 2 + t 2 t - 2 2

f ' t =   - t 2 + 4 t - 2 t 2 - 4 t + 4

Prontinho! Aí está nossa derivada😊

Passo 2

Tá falando pra conferir com um software, então vamos ver no CAS do Geogebra (só porque pediram né...)

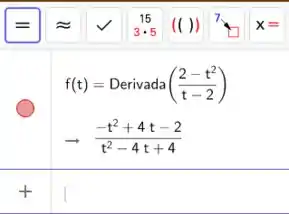
Nossa derivada tá certinha! (como esperávamos né...)

Resposta

f ' t =   - t 2 + 4 t - 2 t 2 - 4 t + 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Derive a função: y = 4 π ² ²