Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 16
Encontre a antiderivada mais geral da função. (Verifique sua resposta diferenciando.)
Passo 1
E aí, blz? Esse problema nos dá a função:
E pede pra a gente calcular a sua antideridava. Mas o que que é isso?!
A antiderivada é o inverso da derivada, mais ou menos como multiplicação e divisão, sabe?! Então se eu derivo a antideridade de , vamos chamar ela de , eu tenho que chegar novamente em .
Primeira coisa: toda vez que você ler antiderivada, saiba que o problema está pedindo nada mais nada menos que a integral da função.A antiderivada também é chamada de primitiva e essa tabelinha vai nos ajudar a resolver o nosso problema:
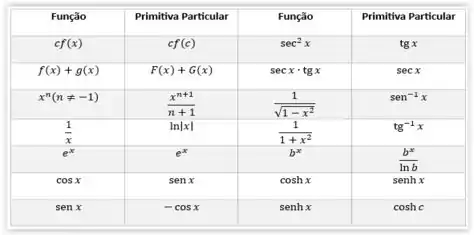
O enunciado nos pediu a antiderivada mais geral da função. Isso significa que a gente vai precisar adicionar uma constante na primitiva particular. Isso porque a derivada de uma constante é igual a zero!
Quando integramos, precisamos sempre lembrar da constante. Mas por que dela? Lembra que a derivada de uma constante é ? Quando integramos,Então quando calculamos a primitiva não temos como garantir que não exista uma constante ali, por isso sempre temos que colocá-la. ☺
Em resumo, a constante de integração é como um “ajuste vertical” que nos permite encontrar a função original a partir da sua taxa de mudança (derivada). É um detalhe importante para garantir que nossa resposta seja completa e abranja todas as possibilidades (a antiderivada mais geral). 😊
Pra resolver esse problema vamos identificar o tipo da nossa função na tabela acima e aplicar para o nosso caso!
Agora vamos lá resolver essa questão!
Passo 2
Queremos achar as funções tais que . Traduzindo que achar a função, que a sua derivada será a função do enunciado.
Vamos trabalhar com a função do enunciado, primeiro vamos simplificá-la realizando a divisão por em todas os termos:
Sabemos que para potências de encontramos a integral da seguinte maneira:
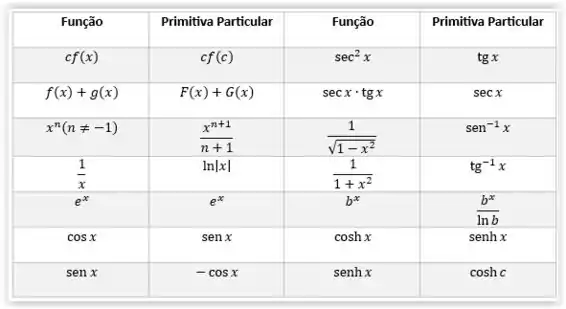
E que esse resultado não funciona para , pois nesse caso temos , que possui integral , já que . Observe a tabela abaixo:
, assim sua primitiva será:
Passo 3
Então, aplicando o método de integração, temos:
A sua antiderivada será:
Passo 4
Vamos conferir se fizemos tudo certinho? Agora derivando, devemos chegar novamente a original do enunciado, podemos usar a tabela do passo 2 para nos ajudar:
O precisa ser avaliado quando derivamos, pois pode ter valores positivos ou negativos dentro do módulo:
Para :Derivando
Para :
Temos um passo a mais, temos que aplicar a regra da cadeia, lembra dela? A derivada de fora multiplicada pela derivada de dentro, dessa forma:
É exatamente o que fizemos aqui:
Como chegamos à mesma função do enunciado, acertamos a nossa questão!
