Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 13
(a) Aproxime por uma série polinomial de Taylor, com grau no ponto .
(b) Use a desigualdade de Taylor para estimar a precisão da aproximação quando está no intervalo dado.
(c) Verifique o resultado da parte anterior fazendo o gráfico de .
Passo 1
Faaala galera, tudo bem?
Essa questão solicita três itens.
No item (a) precisamos aproximar por uma série polinomial de Taylor, com grau no ponto . Já no item (b) usar a desigualdade de Taylor para estimar a precisão da aproximação quando está no intervalo dado. Por fim, no item (c) verificar o resultado da parte anterior fazendo o gráfico de .
Como podemos resolver essa? Pensa comigo!!!
Para o item (a) vamos aplicar a série de Taylor conforme os dados fornecidos. A série é:
Vamos precisar encontrar o valor de cada (derivada aplicada no ponto ), e determinar a expressão . É interessante fazer uma tabela, para ficar organizado e de fácil compreensão.
Para o item (b), vamos aplicar a formula da desigualdade de Taylor:
Por fim, no item (c) precisamos fazer o gráfico de que encontramos no item (b).
Bora lá colocar mão na massa!!!
Passo 2
Item (a).
Vamos encontrar a série de Taylor para a seguinte situação:
A série de Taylor é:
A ideia agora, é expandir a série de Taylor até . Mas vamos expandir até , pois vamos utilizar esse resultado para avaliar na desigualdade de Taylor se a serie esta decaindo ou não.
A tabela a seguir mostra os valores para cada :
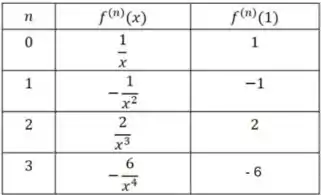
Dessa forma, a série de Taylor para é dada por:
Simplificando, vamos ter:
Passo 3
Vamos para o item (b).
Agora, usando a desigualdade de Taylor, temos que:
Sendo que .
Dessa forma, como o intervalo fornecido no enunciado é , então temos que:
Conforme a tabela do passo 2, temos que está decaindo no intervalo , podemos pegar o maior valor nesse intervalo como sendo:
Sendo assim, substituindo esse valor para , obtemos:
Passo 4
Por fim, vamos fazer o item (c).
Precisamos determinar o gráfico de:
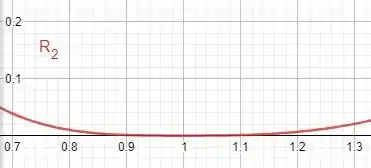
A seguir temos o gráfico de:
Onde,
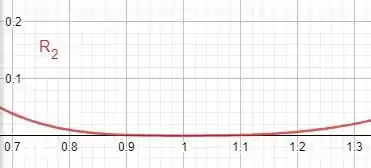
De acordo com o gráfico, o erro aparenta ser menor do que 0,05 no intervalo especificado.
Resposta
