Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 25
Esboce a área da região que está dentro da primeira curva e fora da segunda curva.
Passo 1
Eaee, tudo certinho contigo??
Seguinte... O problema pede para acharmos a área da região dentro da curva e fora da curva .
De forma mais didática, a gente quer calcular a seguinte área em vermelho:
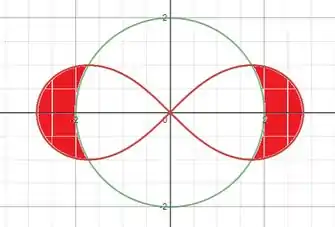
E como fazemos isso???
Através da seguinte integral da área :
Assim, se observamos bem a figura, a área em vermelho é a área de fora (área da figura ) menos a área do círculo.
Agora bora aplicar!! 😉
Passo 2
Note que a primeira curva pode ser escrita como
Assim, devemos ter
Como a primeiro curva tem duas partes, com e , ela terá dois laços simétricos. Já a segunda curva é o círculo de raio :
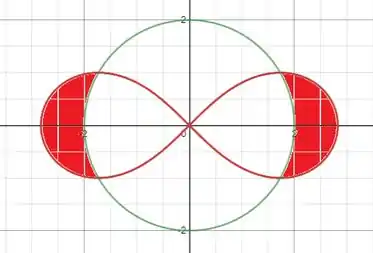
Como a figura é simétrica, vamos calcular a área da região da direita e multiplicar por . Para isso, precisamos achar onde as curvas se encontram:
Obtemos
Esses serão os nossos limites de integração!!!
Passo 3
Como temos que fazer a área entre as curvas, fazemos a área da curva de fora menos a de dentro.
Assim, fazendo a integral para a área de fora, temos que , portanto:
Assim,
Passo 4
Já da curva de dentro, fazendo , temos::
Passo 5
Nesse sentido, temos que a área que queremos calcular é dada por:
Assim,
Logo,