Encontre a área da região dentro de um laço da curva:

Olá, meu grande amigo. Vou te ajudar a resolver essa atividade.

A gente tem a curva:

E queremos calcular a área dentro do laço dessa figura. A gente vai antes de tudooo, visualizar a figura, isso ajuda na resolução do problema. Aqui eu vou utilizar o GeoGebra para gerar o gráfico da figura.

A curva dada possui a seguinte forma:

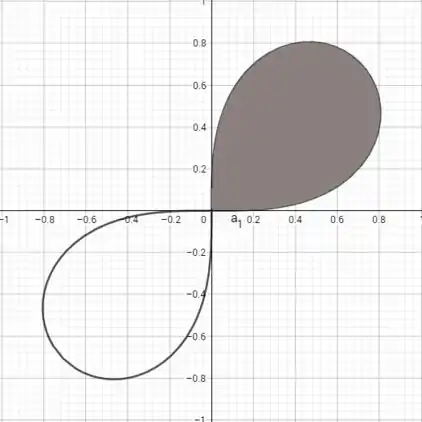
Veja que a gente tá em coordenadas cilíndricas, então a área é dada por:

E a gente precisa encontrar os limites de integração, o que a gente pode fazer, é ver que toda a área da primeira pétala é varrida pelo ângulo de a . Então esse é o nosso limite de integração. Você pode ver abaixo como o varre nossa curva.

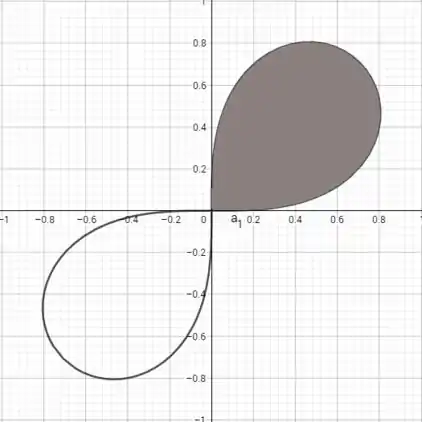
Outra forma de encontrarmos os limites de integração é:

A curva passa pela origem quando seu raio é 0, dessa forma podemos buscar quando isso ocorre duas vezes, pois assim temos a criação da pétala, e o seu fechamento:

Dessa forma, nossos limites de integração são .