Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.5 - Ex. 14

Encontre as áreas das regiões nos Exercícios 9-18

Dentro do círculo r = 3 a cos ⁡ θ e fora da cardioide r = a 1 + cos ⁡ θ ,   a > 0 .

Passo 1

Fala gente tudo bem? Exercício super direto de aplicação, primeiro vamos encontrar a figura a partir do geogebra para entender do que se trata e delimitar os limites e depois, só precisamos botar na fórmula do calculo da área a partir da integral.

A = ∫ β α 1 2 ( r a 2 - r b 2 ) d θ

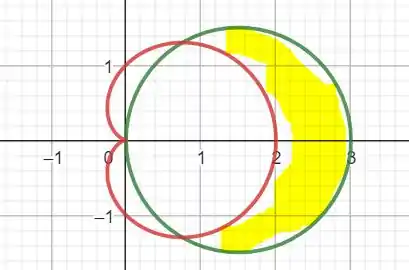Essa é a nossa figura:

Temos 2 regiões distintas com limites diferentes, vamos calcula-los então:

r = r

3 acos ⁡ θ = a ( 1 + cos ⁡ θ )

cos ⁡ θ = 1 2

θ = π 3

Portanto, π / 3 é o nosso ponto de intersecção. Assim, os limites vão de 0 a π 3 , ainda pela questão da simetria do eixo y temos que multiplicar a área por 2.

Passo 2

A = 2 ∫ 0 π 3 1 2 3 acos ⁡ θ 2 - a 2 1 + cos ⁡ θ 2 d θ

A = ∫ 0 π 3 9 a 2 cos 2 ⁡ θ - a 2 - 2 a 2 cos ⁡ θ - a 2 cos 2 ⁡ θ d θ = ∫ 0 π 3 8 a 2 cos 2 ⁡ θ - 2 a 2 cos ⁡ θ - a 2 d θ

A = ∫ 0 π 3 8 a 2 1 + cos ⁡ 2 θ 2 - 2 a 2 cos ⁡ θ - a 2 d θ

A = ∫ 0 π 3 4 a 2 + 4 a 2 cos ⁡ 2 θ - 2 a 2 cos ⁡ θ - a 2 d θ = ∫ 0 π 3 3 a 2 + 4 a 2 cos ⁡ 2 θ - 2 a 2 cos ⁡ θ d θ

A = ∫ 0 π 3 3 a 2 d θ + ∫ 0 π 3 4 a 2 cos ⁡ 2 θ d θ - ∫ 0 π 3 2 a 2 cos ⁡ θ d θ

A = 3 a 2 θ + 2 a 2 s e n   2 θ - 2 a 2 s e n   θ 0 π 3

A = π a 2 - 0 + 2 a 2 ⋅ 1 2 - 0 - 2 a 2 ⋅ 3 2 + 0

A = a 2 π + 1 - 3  

Bora para a próxima!

Resposta

A = a 2 π + 1 - 3  

Exercícios de Livros Relacionados

Dê algumas parametrizações típicas para retas, círculos, parábolas, elipses e hipérboles. Quanto uma curva parametrizada poderia ser diferente do gráfico de sua equação cartesiana?
Como você pode algumas vezes encontrar a área delimitada por uma curva parametrizada e um dos eixos coordenados?
Qual é a fórmula para o coeficiente angular d y d x de uma curva parametrizada x=f ( t ) ,y=g ( t ) ? Quando a fórmula é aplicada? Quando você pode esperar conseguir encontrar d 2 y d x 2 também? Dê e
Cone O segmento de reta que une a origem ao ponto (h, r) é girado sobre o eixo x para gerar um cone de altura h e base de raio r. Encontre a área de superfície do cone com as equações paramétricas x =
Tronco de cone O segmento de reta unindo os pontos (0, 1) e (2, 2) é girado em torno do eixo x para gerar um tronco de cone. Encontre a área de superfície do tronco de cone utilizando a parametrização