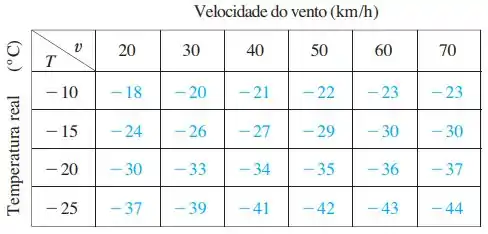
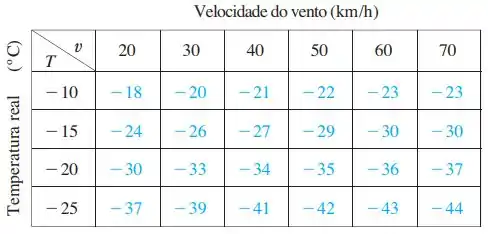
Uma tabela de valores do índice de sensação térmica é dada no Exercício 3 da Seção 14.3. Use-a para estimar o valor de , onde .
Passo 1
Fala galerinha!
A questão dá pra gente uma tabela como substituto da função
E nos pede para encontrar a derivada direcional no ponto e na direção
Para calcular a derivada direcional de uma função num ponto em uma direção unitária nós usaríamos a fórmula
Onde é o gradiente (conjunto das derivadas parciais) da função!
Mas veja que não temos a função exata de ! Dessa forma, para encontrar as derivadas e no ponto nós podemos calcular a inclinação da função usando os dados da tabela!
Porém o incremento entre cada valor de temperatura e velocidade no gráfico é considerável. Por exemplo, quando , a tabela nos dá os pontos “vizinhos” e .
Dessa forma, para aumentar a aprecisão da nossa derivada, será interessante fazer a média entre a inclinação à esquerda e à direita do nosso ponto!
Passo 2
A fórmula que desejamos definir é
Onde e .
Substituindo o gradiente:
E o vetor unitário:
Fazendo o produto escalar, temos:
Passo 3
Para encontrar nós podemos calcular a inclinação da função, mantendo constante, usando os valores da tabela! De forma que
Usando os pontos e
E usando os pontos e
Tirando a média entre esses dois valores nós obtemos
Passo 4
Analogamente, agora vamos encontrar
Usando os pontos e
Usando os pontos e
Tirando a média
Passo 5
Substituindo de volta na fórmula da derivada direcional