Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 21

Encontre a área da região dentro de um laço, onde r = 1 + 2 s e n θ .

Passo 1

Fala ai, tudo tranquilo?

Preparei alguns passos para te ajudar a entender como iremos resolver esta questão.

Se liga em!

Para encontrar a área da região dentro do laço definido pela equação r = 1 + 2 s e n ( θ ) , utilizamos a fórmula da área em coordenadas polares:

∫ a b 1 2 r θ 2 d θ

onde f ( θ ) é a equação da região.

O procedimento é:

  1. Constuimos o gráfico para saber qual região estamos trabalhando.
  2. Encontramos os pontos de interseção da região consigo mesma para determinar os limites de integração a e b .
  3. Calculamos f ( θ ) = 1 + 2 s e n ( θ )   e substituímos na fórmula da área.
  4. Calculamos a integral ∫ a b 1 2 r θ 2 d θ para obter a área da região dentro do laço.

Passo 2

Utilizando um programa para a contrução do gráfico. Temos

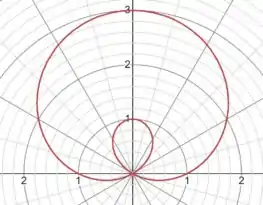
Passo 3

Nessa função, teremos um laço dentro outro: se o seno for negativo teremos um laço menor e se o seno for positivo teremos um laço maior, tudo por causa da soma de um número na função.

Como queremos o seno negativo, temos o intervalo [ π , 2 π ] , nele o seno zera nos extremos e e negativo.

Passo 4

Como a expressão do raio e dada, já podemos calcular a integral:

∫ a b 1 2 r θ 2 d θ

Substituindo a função r :

∫ π 2 π 1 + 2   s e n θ 2 2 d θ

Aplicando o quadrado dessa soma:

∫ π 2 π 1 + 4 s e n θ + 4 s e n θ 2 2 d θ  

E separando as integrais:

∫ π 2 π 1 2 d θ + ∫ π 2 π 4 s e n θ 2 d θ + ∫ π 2 π 4 s e n θ 2 2 d θ  

Vamos resolver uma integral de cada vez.

Passo 5

- Primeira integral:

∫ π 2 π 1 2 d θ

θ 2 = 2 π - π 2 = π 2

- Segunda integral:

∫ π 2 π 4 s e n θ 2 d θ

- 4 c o s θ 2 = - 2 c o s θ

- 2 c o s 2 π + 2 c o s π

- 2 - 2 = - 4

Passo 6

- Terceira integral:

∫ π 2 π 4 s e n θ 2 2 d θ

Precisamos de uma substituição para resolver essa integral, s e n θ 2 = 1 - cos ⁡ 2 θ 2  

∫ π 2 π 4 2 . 1 - cos ⁡ 2 θ 2 d θ

Simplificando os termos

∫ π 2 π 1 - cos ⁡ 2 θ d θ

θ - s e n   2 θ = 2 π - π + s e n   4 π = π

Passo 7

Somando as partes, temos.

∫ π 2 π 1 2 d θ + ∫ π 2 π 2 s e n θ d θ + ∫ π 2 π 2 s e n θ 2 d θ

π 2 - 4 + π

3 π 2 - 4

Resposta

Logo, a resposta será 3 π 2 - 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região dentro de um laço, onde r = 3 c o s 5 θ .
Encontre a área da região dentro de um laco, onde r = s e n 2 θ .
Esboce a curva e calcule a área limitada por ela r = 3 cos ⁡ θ
Encontre a área da região dentro de um laço, onde r = 4 s e n 3 θ .
Encontre a área da regiao sombreada, onde r = 1 + s e n ( θ ) .