Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 19
Encontre a área da região dentro de um laço, onde .
Passo 1
Em coordenadas polares temos que a área de uma região é dada pela integral
onde r é a função que determina como o raio da curva varia em relação ao ângulo no intervalo .
Teremos que
onde é uma primitiva de
No problema, precisamos identificar o intervalo onde a curva faz um laço, como a função que determina o raio e periódica de período menor que em algum momento ela “se fecha” e esse intervalo sera nosso domínio de integração.
Basicamente temos que descobrir em quais pontos o raio será zero. Pois veja, o raio da figura irá se iniciar zerado, ele irá crescer, chegará a o seu valor máximo e depois irá zerar novamente, então nesse segundo momento que ele zerou, temos uma pétala, então esse primeiro momento e o segundo momento, é o que queremos.
Passo 2
Vamos dar uma olhada na nossa curva:
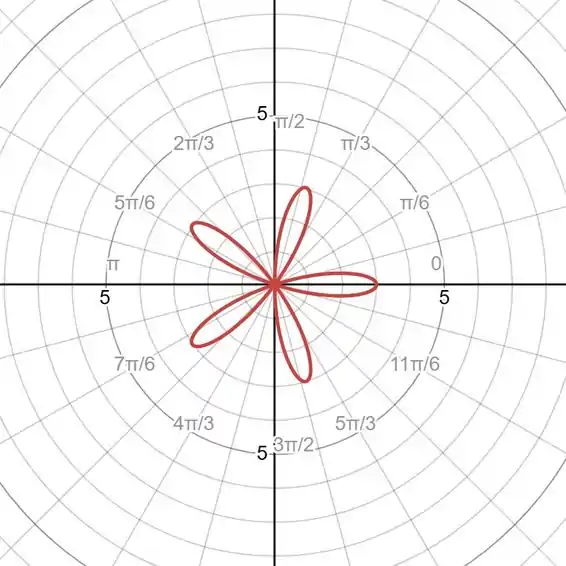
Temos que
Sabemos que o cosseno será zero para esse conjunto de valores, para sendo inteiro.
Então como precisamos apenas de valores, então temos um dos intervalos possíveis para um laço:
Passo 3
Como a expressão do raio e dada, já podemos calcular a integral:
Precisamos de uma substituição para resolver essa integral, vamos lá:
Usando as relações:
e a fórmula do arco duplo do cosseno:
Trocando por , passando o seno ao quadrado para o outro lado, substituindo e simplificando, temos:
Passo 4
Agora, substituindo a expressão na integral e resolvendo:
Realizando a transformação:
Dividindo as integrais:
Usando que uma primitiva da função na segunda integral é , temos
Temos então:
Resposta
Logo, a resposta será .