Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 5

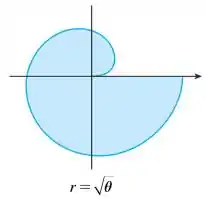
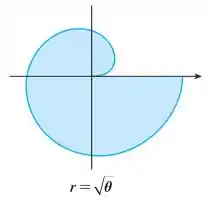
Encontre a área da região sombreada.

Passo 1

Olá, meu amigo. Vamos resolver mais uma atividade juntos.

Vamos aqui calcular a área da curva:

r = θ

Vamos então utilizar a fórmula para a área de uma região cuja fronteira é dada por uma equação polar:

A = ∫ 1 2 r 2 d θ

O r das coordenadas polares é a distância entre a origem e o ponto e o ângulo θ é inclinação desse r em relação a horizontal, abaixo existe uma melhor visualização desse tipo de coordenada e sua relação com as coordenadas cartesianas:

Os limites de integração podemos encontrar a partir da figura. A linha que forma a fronteira do gráfico começa em ( 0,0 ) e dá uma volta completa, ou seja, percorreu um ângulo θ = 2 π   r a d .

Passo 2

Aplicando os limites de integração   0 ≤ θ ≤ 2 π e substituindo r = θ , obtemos:

A = ∫ 0 2 π 1 2 θ   d θ

Retirando a constante da integração:

A = 1 2 ∫ 0 2 π θ   d θ

Realizando a integração:

A = 1 2 θ 2 2 0 2 π

Calculando a área:

A = 1 4   4 π 2 - 0  

Temos então que:

A = π ²

Resposta

A = π ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as áreas das superfícies geradas girando as curvas nos Exercícios 31-34 em torno dos eixos indicados.31. x = c o st ,y = 2 + s e nt ,0 ≤ t ≤ 2 π ,e i x ox
24. Encontre a área sob y = x 3 sobre [ 0,1 ] utilizando as seguintes parametrizações.a) x = t 2 ,y =t 6 . b) x = t 3 ,y =t 9 .
Encontre os comprimentos das curvas nos Exercícios 25-30.26. x = t 3 ,y = 3 t 2 / 2 ,0 ≤ t ≤ 3
Assumindo que as equações nos Exercícios 15-20 definem x e y implicitamente como funções deriváveis x = f ( t ) ,y = g ( t ) , encontre o coeficiente angular da curva x = f ( t ) ,y = g ( t ) no valor
Assumindo que as equações nos Exercícios 15-20 definem x e y implicitamente como funções deriváveis x = f ( t ) ,y = g ( t ) , encontre o coeficiente angular da curva x = f ( t ) ,y = g ( t ) no valor