Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.2 - Ex. 55

Encontre área da região limitada pelas curvas dadas.

y = sin ⁡ x ,     y = sin 3 ⁡ x ,       x = 0 ,       x = π 2

Passo 1

Opa, bora lá! O enunciado nos dá as seguintes curvas:

y = sin ⁡ x ,     y = sin 3 ⁡ x ,       x = 0 ,       x = π 2

E pede pra a gente calcular a área da região delimitada por elas! Para resolvermos esse problema, fazemos algumas considerações: o intervalo é de 0 < x < 2 , mas como sabemos para a função seno 0 < sin ⁡ x < 1 , então, sin 3 ⁡ x < sin ⁡ x .

Podemos esboçar o gráfico dessas curvas pra nos ajudar na visualização:

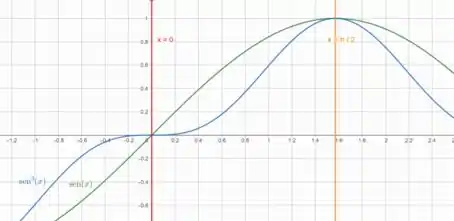
Pra calcularmos essa área delimitada fazemos:

A = ∫ a b f x d x

Essa função aí vai ser:

f x = sin ⁡ x - sin 3 ⁡ x

Isso porque a curva sin ⁡ x esta por cima da sin 3 ⁡ x no intervalo delimitado entre x = π / 2 e x = 0 que vão ser nossos limites de integração. Então:

A = ∫ 0 π 2 ( sin ⁡ x - sin 3 ⁡ x ) d x

Passo 2

Organizamos a integral da seguinte forma:

A = ∫ 0 π 2 sin ⁡ x ( 1 - sin 2 ⁡ x ) d x

Como sin 2 ⁡ x + cos 2 ⁡ x = 1 e sin 2 ⁡ x = 1 - cos 2 ⁡ x , logo:

A = ∫ 0 π 2 sin ⁡ x cos 2 ⁡ x d x

Aplicamos uma substituição e resolvemos a integral!!

Passo 3

Fazendo:

u = cos ⁡ x             d u = - sin ⁡ x d x

Aplicando na integral (não esquece de mudar os intervalos de integração também hein??)

A = ∫ 1 0 u 2 - d u = ∫ 0 1 u 2 d u

A = u 3 3 0 1

Então,

A = ( 1 ) 3 3 - - 0 3 3

A = 1 3

Prontinho!!

Resposta

A = 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 30, calcule a integral indefinida. 18 )∫ sec ⁡ 5 x + c o s e c5 x 2 . d x
Nos Exercícios de 1 a 30, calcule a integral indefinida. 30 )∫ s e c 4 ( w ) t gw . d w
Nos Exercícios de 1 a 30, calcule a integral indefinida. 25 )∫ d u 1 + sec ⁡ ( u 2 )
Nos Exercícios de 1 a 30, calcule a integral indefinida. 24 )∫ t g 4 y sec 5 ⁡ ( y ) . d y
Ache a área da região limitada pela curva y = t g ²x , ² pelo eixo x e pela reta x = 1 4 π .