Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 59
Encontre os valores de tal que a área da região limitada pelas parábolas e seja .
Passo 1
Bora lá! Nosso exercício nos dá as parábolas:
Aqui devemos encontra quem é para que a área entre essas duas curvas seja igual a .
Repara que:
Uma vez que:
São duas parábolas iguais. Só que uma tem concavidade pra cima e outra pra baixo. Assim:
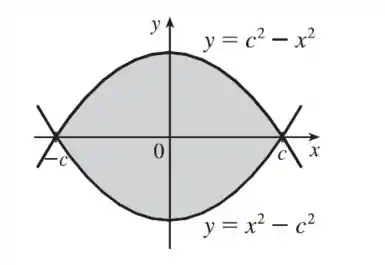
Passo 2
Então a área pode ser calculada por:
Os limites de integração vão ser iguais aos pontos de intersecção das parábolas, que vai ser igual as suas raízes:
Então temos:
Mas isso é igual a:
Pegamos pois sua concavidade é pra baixo, então ela vai tá na parte positiva do eixo .
Passo 3
Temos que:
Integrando:
Aplicando os limites de integração:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Determine o centro de massa do conjunto - 1 ≤ x ≤ 3 e 0 ≤ y ≤ x + 1 2 . (Sugestão: Resolva o problema no plano u , y , com u = x + 1 .)
Calcule o volume do sólido obtido pela rotação da região x 2 + 4 y 2 ≤ 1 , em torno da reta y = 1 .
Calcule o centro de massa da região dada: A=[ ( x , y )∈R ²/x ²+4 y ² ² ² ² ≤ 1 ,x ≥ 0ey ≥ 0 ]
Determine o centro de massa da região A dada.A = { ( x , y ) ∈ R 2 0 ≤ x ≤ 1 ,0 ≤ y ≤ x 3 }
a) Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 tomando como pólo a origem e como eixo polar o semi-eixo O x .b) Escreva, em coordenadas polares, a equação da elipse x 2