Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 6

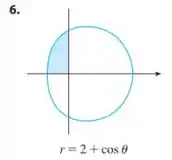
Encontre a área da região sombreada:

Passo 1

Para se calcular uma área em coordenadas polares, é necessário se levar em consideração a área de um setor circular.

Um setor circular possui comprimento C = r θ , sendo r a coordenada radial e θ a coordenada polar dada em radianos. A área de um círculo é dada por A o = π r 2 enquanto a área do setor é

A = 1 2 r 2 θ

Uma função descrita em coordenadas polares possui forma r = f ( θ ) , de modo que para integrar sua área é necessário utilizar a integral

A = ∫ a b 1 2 f θ 2 d θ

Para essa questão precisamos somente resolver esta integral para encontrar a área determinada.

Passo 2

Primeiro iremos definir a integral a ser resolvida e seus intervalos.

Pela figura podemos ver que a região sombreada se encontra no segundo quadrante inteiro, por isso, o intervalo em que o ângulo θ está é π 2 ≤ θ ≤ π . A integral da área então será

A = ∫ π / 2 π 1 2 [ f ( θ ) ] 2 d θ = ∫ π / 2 π 1 2 2 + c o s θ 2 d θ

Passo 3

Agora que definimos a integral que iremos resolver, podemos calculá-la.

Vamos primeiro resolver a integral indefinida e então substituir os limites no final da integração:

A θ = ∫ 1 2 2 + c o s θ 2 d θ

Abrindo o polinômio e colocando a constante para fora

A θ = 1 2 ∫ 4 + 4 c o s θ + c o s 2 θ d θ

Pela linearidade

A θ = 1 2 ∫ 4 d θ + 1 2 ∫ 4 c o s θ d θ + 1 2 ∫ c o s 2 θ d θ

Usando a seguinte propriedade trigonométrica

c o s 2 θ = 1 + c o s 2 θ 2

Ficamos com

A θ = 1 2 ∫ 4 d θ + 1 2 ∫ 4 c o s θ d θ + 1 4 ∫ 1 + c o s 2 θ d θ

Integrando

A θ = 2 θ + 2 s e n θ + θ 4 + s e n 2 θ 8 + c

Tirando MMC

A θ = 18 θ + s e n 2 θ + 16 s e n θ 8 + c

Passo 4

E agora substituímos os limites:

A   = 18 π + s e n 2 π + 16 s e n π 8 - 18 π / 2 + s e n 2 π 2 + 16 s e n π 2 8

A = 9 π - 16 8

Resposta

A = 9 π - 16 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região dentro de um laço, onde r = 4 s e n 3 θ .
Encontre a área da regiao sombreada, onde r = 1 + s e n ( θ ) .
Encontre a área da regiao sombreada, onde r = 4 + 3 s e n ( θ ) .
Seja R a região dentro do laço da curva no Exemplo 1:Calcule a área de R Se R girar em torno do eixo x , encontre o volume do sólido resultante Encontre o centroide de R
Uma vaca é amarrada a um silo com raio r por uma corda comprida o suficiente para alcançar apenas o outro lado do silo. Calcule a área disponível para a vaca pastar.