Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 5

É dada a tabela de valores de uma função f x , y definida em R = 1,3 × 0,4 .

  1. Estime ∬ R f x , y d A utilizando a Regra do Ponto Médio com m = n = 2 .
  2. Estime a integral dupla com m = n = 4 , escolhendo como pontos amostrais os pontos mais distantes da origem.

x

y

0

1

2

3

4

1,0

2

0

- 3

- 6

- 5

1,5

3

1

- 4

- 8

- 6

2,0

4

3

0

- 5

- 8

2,5

5

5

3

- 1

- 4

3,0

7

8

6

3

0

Passo 1

  1. Primeiro vamos ver na figura abaixo os subretângulos que vamos usar:

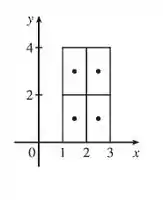
    2. Temos que a superfície é o gráfico de f x , y = x y e vamos ter que ∆ A é a área de cada retângulo, então ∆ A = 1.2 = 2 , e que m = n = 2 , então a regra do ponto médio, pegando o ponto do intervalo utilizado, que vai ser o ponto médio de cada intervalo:

    ∬ R f x , y d A ≈ ∑ i = 1 2 ∑ j = 1 2 f x - , y - ∆ A = f 1 . 5 , 1 ∆ A + f 1 . 5 , 3 ∆ A + f 2.5 , 1 ∆ A + f 2.5 , 3 ∆ A = 1.2 + - 8 . 2 + 5.2 + - 1 . 2 = - 6

    Passo 2

  2. Agora vamos ver na figura abaixo os subretângulos que vamos usar:

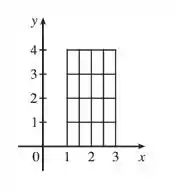
Temos que a superfície é o gráfico de f x , y = x y e pegando o ponto do intervalo utilizado, que vai ser o ponto mais distante da origem, que é o conto superior direito de cada intervalo, vamos ter que ∆ A é a área de cada retângulo, então ∆ A = 1 . 1 2   = 1 2 , e com m = n = 4 temos :

∬ R f x , y d A ≈ ∑ i = 1 4 ∑ j = 1 4 f x i , y i ∆ A = f 1.5,1 ∆ A + f 1.5 , 2 ∆ A + f 1 . 5 , 3 ∆ A + f 1 . 5 , 4 ∆ A + f 2 , 1 ∆ A + f 2,2 ∆ A + f 2,3 ∆ A + f 2,4 ∆ A + f 2.5,1 ∆ A + f 2.5 , 2 ∆ A + f 2.5 , 3 ∆ A + f 2.5 , 4 ∆ A + f 3 , 1 ∆ A + f 3,2 ∆ A + f 3,3 ∆ A + f 3,4 ∆ A = 1 . 1 2   + - 4 . 1 2 + - 8 . 1 2 + - 6 . 1 2 + 3 . 1 2 + 0 . 1 2 + - 5 . 1 2 + - 8 . 1 2 + 5 . 1 2 + 3 . 1 2 + - 1 . 1 2 + - 4 . 1 2 + 8 . 1 2 + 6 . 1 2 + 3 . 1 2 + 0 . 1 2 = - 3 . 5

Resposta

  1. ∬ R f x , y d A = - 6
  2. ∬ R f x , y d A = - 3.5
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada.int_0^2 int_0^(pi // 2) ( x s e n y ) d y d x
Calcule a integral iterada.int_0^1 int_1^2 ( 4 x^3 - 9 x^2 y^2 ) d y d x
∬_R (y + x y^(- 2)) d A , R = { ( x , y ) | 0 = x = 2 , 1 = y = 2 }
Calcule a integral iterada.int_1^4 int_0^2 ( 6 x^2 - 2 x ) d y d x
int_0^1 int_0^1 v (u - v^2)^4 d u d v