Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 14
Encontre a área da superfície com precisão de quatro casas decimais, expressando a área em termos de integral de função de uma variável real e use sua calculadora para estimar a integral.
A parte da superfície que está dentro do cilindro .
Passo 1
E aii, pessoal!
Nessa questão precisamos calcular a área de uma superfície que ela descreveu, com precisão de quatro casas decimais. Mas antes, precisamos expressar essa área como uma integral simples, e usar uma calculadora pra encontrar o valor dela.
Bom, precisamos lembrar que a área da superfície que é o gráfico da função é calculada assim:
Então o que vamos fazer é encontrar quem é , pra calcular as derivadas parciais e substituir na fórmula.
Depois, nosso problema vira transformar essa integral dupla em uma integral simples, pra calcularmos!
Passo 2
Primeiro, vamos voltar pra nossa superfície:
A parte da superfície que está dentro do cilindro
Como estamos falando da superfície , essa vai ser nossa função:
O cilindro vai servir pra limitar essa função em um domínio .
Então vamos calcular as derivadas parciais. Lembrando que quando derivamos em função de uma variável, as demais ficam constantes:
Vamos ter que fazer a regra da cadeia:
Agora em função de :
De novo usando a regra da cadeia:
Substituindo na nossa fórmula:
Podemos abrir os quadrados:
E colocar em evidência:
Passo 3
Agora vamos olhar para o nosso domínio , que é limitado pelo cilindro . No plano , isso é um círculo de centro na origem e raio :
Então podemos fazer uma mudança de variável para coordenadas polares.
Para isso, vamos fazer as seguintes mudanças:
Como estamos no círculo inteiro, e de raio , os limites de e ficam:
Além disso, vamos lembrar que quando fazemos essa mudança de variáveis, a gente tem essa relação aqui:
Ela vem do .
Então vamos voltar pra integral:
Agora a gente pode fazer a mudança de variáveis, sem esquecer de multiplicar o jacobiano, que em coordenadas polares é .
Nossa integral fica assim:
Colocando os limites de integração de e :
Passo 4
Agora precisamos transformar isso em uma integral de uma variável.
Percebe que o integrando só depende de :
E a primeira integral é em função de ! Então podemos tirar esse integrando todo da primeira derivada:
Resolvendo essa integral:
Então a integral que define a nossa área é essa:
Vamos usar o WolframAlpha pra calcular isso:
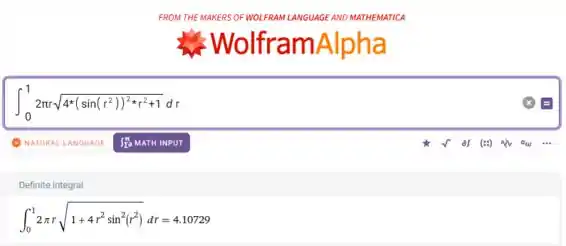
Então temos que