Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.5 - Ex. 2
Encontre a área da superfície.
A parte do plano que está dentro do cilindro .
Passo 1
Faala, pessoal!!
Nessa questão temos que achar a área de uma superfície!
Pra isso, a gente vai usar essa fórmula:
Que da a área de uma superfície definida pelo gráfico de em um domínio
Nossa missão vai ser encontrar quem é esse , calcular as derivadas parciais e jogar na fórmula. Depois, a gente vai ter uma integral pra calcular! Vamos descobrir quem é e calcular essa integral normalmente.
Passo 2
Como a gente quer uma função que o gráfico dê esse plano do enunciado, vamos isolar o na equação do plano:
Agora vamos calcular as derivadas parciais. Lembrando que quando derivamos em função de uma variável, consideramos a outra constante:
Agora em função de :
Substituindo na nossa fórmula:
Então:
Como é constante, sai da integral e fica assim:
Mas a gente pode calcular a área de uma região no plano assim:
Então a área da superfície fica:
Basta calcularmos a área de , que achamos a área da superfície!
Passo 3
Como a nossa parte do plano está dentro de um cilindro , o domínio vai ser a projeção dessa superfície no plano , vai ser um círculo de raio :
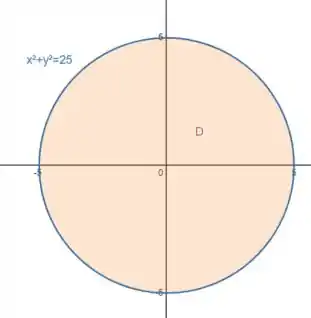
Como queremos a área dessa região, calculamos:
Então, a área da superfície será: