Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 42

Encontre as assíntotas horizontais e verticais

y = 1 + x 4 x 2 - x 4

Passo 1

Olá, meu querido amigo.

Nessa questão vamos encontrar as assíntotas horizontais e e verticais da função:

y = 2 x 2 + x - 1 x 2 + x - 2

Lembrando que pra achar assíntotas horizontais fazemos o limite da função com x tentendo para mais infinito e para menos infinito. Se esses limites derem um número bonitinho chamado L , a reta y = L será assíntota horizontal.

Já para achar assíntotas verticais vamos procurar pontos em que a função não esteja definida, tipo pontos que fazem ter divisão por zero, ou log negativo ou igual a zero, ou raiz negativa...

Daí fazemos o limite da função com x tendendo a esses pontos. Aí aqui é diferente... se o limite for pra mais ou menos infinito então as retas verticais nesses pontos serão serão assíntotas verticais.

Passo 2

Para encontrar a assíntota horizontal, tomaremos o limite da função quando x → ± ∞ .

Lembrando que uma boa técnica pra resolver limites quando x está tendendo para mais ou menos infinito é colocar o x com maior expoente em evidência:

lim x → ± ∞ ⁡ 1 + x 4 x 2 - x 4 = lim x → ± ∞ ⁡ x 4 1 x 4 + x 4 x 4 x 4 x 2 x 4 - x 4 x 4

= lim x → ± ∞ ⁡ 1 x 4 + 1 1 x 2 - 1

= 0 + 1 0 - 1

= - 1

Logo, y = - 1 é uma assíntota horizontal.

Passo 3

Para encontrar a assíntota vertical vamos pegar as restrições. Como só temos uma fração, então a única preocupação é quando o denominador for igual a zero, né?

Vamos achar para quais valores de x o denominador vira zero:

x 2 - x 4 = 0

Repara que podemos colocar x 2 em evidência:

x 2 1 - x 2 = 0

Como temos o produto de dois polinômios, então ou um vai ser igual a zero ou o outro. Daí temos duas equações pra resolver:

- primeira equação:

x 2 = 0

x = 0

- segunda equação:

1 - x 2 = 0

x 2 = 1

x = ± 1

(não esquece que o quadrado quando passa pro outro lado como raiz é “mais ou menos” a raiz, heim!?)

Então agora calculamos os limites de x tendendo a 0, de x tendendo a - 1 e de x tendendo a 1 .

Passo 4

Para o limite de x tendendo a 0 :

lim x → 0 ⁡ 1 + x 4 x 2 - x 4 = 1 + 0 0 - 0

= 1 0

= ∞

Como o limite vai pra mais infinito, então x = 0 é uma assíntota vertical.

Para o limite de x tendendo a - 1 :

lim x → - 1 ⁡ 1 + x 4 x 2 - x 4 = 1 + - 1 4 - 1 2 - - 1 4

= 1 + 1 1 - 1

= 2 0

= ∞

Como o limite vai pra mais infinito, então x = - 1 é uma assíntota vertical.

Para o limite de x tendendo a 1 :

lim x → - 1 ⁡ 1 + x 4 x 2 - x 4 = 1 + 1 4 1 2 - 1 4

= 1 + 1 1 - 1

= 2 0

= ∞

Como o limite vai pra mais infinito, então x = 1 é uma assíntota vertical.

Passo 5

Mostraremos agora uma comprovação gráfica do resultado obtido. Usando alguma ferramenta pra plotar o gráfico:

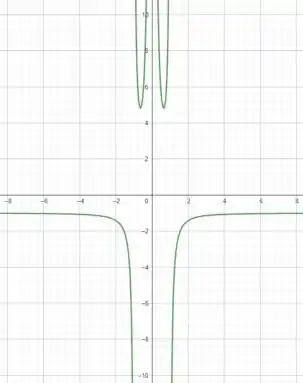
Agora se traçarmos as linhas que achamos como assíntotas (a reta y = - 1 em azul, x = 1 em vermelho e x = - 1 em laranja):

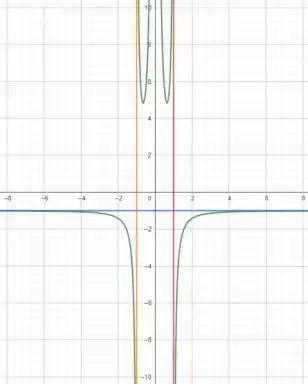
Resposta

y = - 1 é uma assíntota horizontal

x = 0   e   x = ± 1 é uma assíntota vertical

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19. Encontre o limite ou demonstre que não existe. lim t → ∞ ⁡ t + t 2 2 t - t 2
Encontre o limite ou demonstre que não existe.underset(x - oo)(lim) ((2 x^2 + 1)^2)/((x - 1)^2 ( x^2 + x ))
Encontre o limite ou demonstre que não existe. l i m y → ∞2-3 y 2 5 y 2+4 y
29. Encontre o limite ou demonstre que não existe. lim x → ∞ ⁡ x 4 - 3 x 2 + x x 3 - x + 2
5. Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas: lim x → 0 ⁡ f x = - ∞ lim x → - ∞ ⁡ f x = 5lim x → ∞ ⁡ f x = - 5