Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 44
Encontre as assíntotas horizontais e verticais
Passo 1
Fala aí, pessoal.
Aqui nos é dada a função
e a partir disso iremos encontrar as assíntotas verticais e horizontais da função.
Então, vamos ver como fazer isso.
Pela definição,
A reta é chamada de assíntota horizontal da curva se
ou
Então quando tomamos o limite ao infinito da função, e encontramos um valor , este valor é a assíntota horizontal da função. Beleza?
E para encontrar a assíntota vertical é muito simples, devemos pensar o seguinte:
“De que ponto , os valores de se aproximam que fazem a função ‘explodir’ para infinito” (podem ser um ou mais pontos)?”
Se existir esse valor de que, ele será nossa assíntota vertical.
Vamos aplicar isso a nossa função.
Passo 2
Para encontrar a assíntota horizontal, tomaremos o limite da função quando
Começado com
Logo, é uma assíntota horizontal.
E para
Logo, também é uma assíntota horizontal
Passo 3
Para encontrar a assíntota vertical é muito simples, devemos pensar o seguinte:
“De que ponto , os valores de se aproximam que fazem a função ‘explodir’ para infinito” (podem ser um ou mais pontos)?”
ou seja,
Para encontrar o valor de igualaremos o denominador a , pois isso fará nossa função explodir, e calcularemos o valor de . Então:
Logo, é uma assíntota vertical.
Passo 4
Mostraremos agora uma comprovação gráfica do resultado obtido
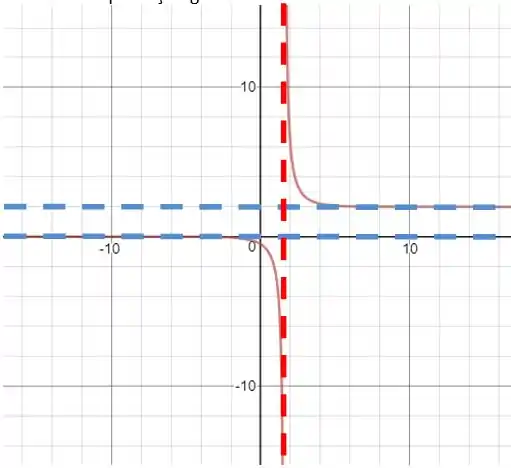
Resposta
é uma assíntota horizontal
é uma assíntota vertical