Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.3 - Ex. 48
(a) Encontre as assíntotas vertical e horizontal.
(b) Encontre os intervalos nos quais a função é crescente ou decrescente.
(c) Encontre os valores máximos e mínimos locais.
(d) Encontre os intervalos de concavidade e os pontos de inflexão.
(e) Use a informação das partes (a)-(d) para esboçar o gráfico de .
Passo 1
Oi galerinha, bora resolver mais uma?
Vamos resolver cada parte da questão para a função
(a) Assíntotas Verticais e Horizontais
A tangente tem assíntotas verticais onde seu argumento é para qualquer inteiro .
No intervalo dado a tangente tem uma assíntota vertical em
Portanto, as assíntotas verticais são:
#### Assíntotas Horizontais
Para verificar as assíntotas horizontais, analisamos o comportamento da função quando
Note que tende a infinito nesses pontos e, portanto, também não tende a um valor finito.
Portanto, não há assíntotas horizontais.
Passo 2
(b) Intervalos de Crescimento e Decrescimento
Para determinar os intervalos de crescimento e decrescimento, encontramos a derivada de
Usando a regra do produto:
Para encontrar os intervalos de crescimento e decrescimento, analisamos o sinal de
Precisamos determinar onde
Passo 3
Essa equação não tem uma solução analítica simples. No entanto, podemos analisar o sinal de qualitativamente.
Para
- é negativa.
- é negativa.
- é positiva.
Portanto, pode ser analisado para verificar o comportamento de crescimento ou decrescimento, mas isso pode ser feito numericamente.
Para
- é positiva.
- é positiva.
- é positiva.
Portanto,é positiva e a função é crescente nesse intervalo.
Para um ponto mais preciso, podemos resolver a equação numericamente para encontrar a mudança de sinal.
Passo 4
(c) Valores Máximos e Mínimos Locais
Como não possui uma solução analítica simples, determinamos os pontos críticos numericamente e verificamos o comportamento da função nesses pontos.
(d) Intervalos de Concavidade e Pontos de Inflexão
Para determinar os intervalos de concavidade e os pontos de inflexão, encontramos a segunda derivada
Usando a regra do produto e a regra da cadeia:
Para determinar a concavidade:
- indica concavidade para cima.
- indica concavidade para baixo.
Analisamos o sinal de
- Para próximo de indicando concavidade para cima.
- Para , a análise numérica pode indicar mudança na concavidade.
Passo 5
Assíntotas:
- Verticais:
- Horizontais: Nenhuma
Intervalos de Crescimento e Decrescimento:
- Crescente:
- Decrescente:
Valores Máximos e Mínimos Locais:
- Nenhum valor m��ximo ou mínimo local evidente sem análise numérica.
Intervalos de Concavidade e Pontos de Inflexão:
- Concavidade para cima: Verificação numérica necessária.
Passo 6
(e) Esboço do Gráfico
Com base nas informações:
- A função tem assíntotas verticais em .
- A função é decrescente para e crescente para .
- A função é côncava para cima em alguns intervalos.
Aqui está um esboço aproximado do gráfico de
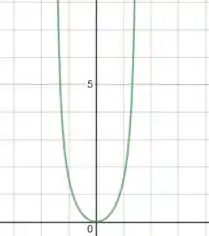
Resposta
Vide o passo a passo.