Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 70
Use o roteiro para esboçar o gráfico da curva. No passo D, ache a equação para assíntota oblíqua.
Passo 1
Falaaa aeee, vamos para mais uma questão?
Nós temos a função
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
Verificar se há simetria ímpar, isso é:
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
Aqui também vamos procurar por assíntota oblíqua. Para isso basta dividir o numerador pelo denominador da função. O quociente encontrado se for uma função de primeiro grau é uma assíntota oblíqua.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
O primeiro passo (A) é determinar o domínio da função. Ou seja, os pontos onde não há problema, nesse caso, como a função está bem definida em qualquer ponto (não estaríamos dividindo algum termo por zero, por exemplo), temos:
Passo 3
O segundo passo (B) é encontrar as interseções com os eixos coordenados.
Com o eixo :
Não intercepta o eixo , pois:
O que não é verdade para nenhum .
Passo 4
O terceiro passo (C) é determinar a simetria, ou seja, se a função é par ou ímpar. No nosso caso, a função não é par e nem ímpar, pois para temos que . Logo, nossa função é antissimétrica.
Passo 5
O quarto passo (D) é encontrar as assíntotas.
Percebe-se que como está bem definida, então não temos assíntotas verticais.
Agora, precisamos achar a assíntota obliqua.
Como,
Você não precisa se preocupar em fazer a divisão de polinômios. Basta perceber que aqui temos uma equação de reta que está multiplicando por uma função que quando tende a ela tende a zero, logo:
Portanto temos que:
Daí,
Então a reta é a assíntota obliqua.
Passo 6
Vamos para o passo (E). Ou seja, achar os intervalos onde a função é crescente ou decrescente além de nossos candidatos a máximo e mínimo.
Para isso, façamos:
Perceba que:
Então é crescente em e decrescente fora, ou seja, em .
Passo 7
No passo (F), devemos usar o teste da primeira derivada. Ou seja, achar os máximos e mínimos, se eles existirem.
Como sai de decrescente para crescente em o ponto mínimo local é:
Não existe máximo.
Passo 8
Vamos ao penúltimo passo, o (G). Aqui devemos analisar a concavidade da função, para isso façamos:
Temos que para qualquer , ou seja, é sempre côncava para cima. (você pode testar isso atribuindo valores para .)
Passo 9
Aqui vamos juntar todos os passos, ou seja, vamos desenhar o gráfico.
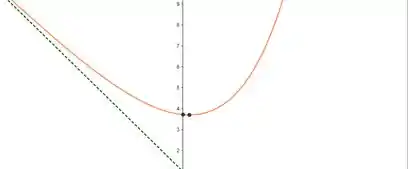
Resposta
Portanto, o esboço dessa função é:
