Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.6 - Ex. 14

Encontre o centro de massa e o momento de inercia em relação ao eixo x de uma placa fina delimitada pelas curvas x = y 2 x = 2 y - y 2 se a densidade no ponto (x,y) for δ x , y = y + 1 .

Passo 1

Faaaala, cara! Tranquileba?

Pelo gráfico das funções temos:

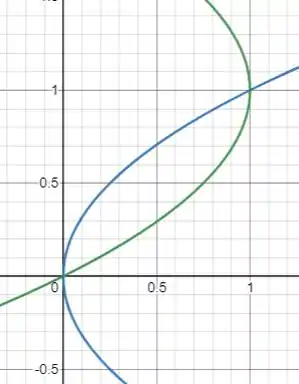
E podemos notar que:

y ∈ 0,1

E sendo x dado por y:

x ∈ y 2 , 2 y - y 2

Logo temos tudo o que precisamos para calcualr o centro de massa, dado por:

M x   o u   y = ∬ δ x , y x   o u   y   d x   d y ∬ δ x , y d x   d y

E os momentos de inércia.

Passo 2

Para M :

M = ∫ 0 1 ∫ y 2 2 y - y 2 y + 1 d x   d y

∫ 0 1 y + 1 x y 2 2 y - y 2 d y

2 ∫ 0 1 ( ( y + 1 ) ( y - y 2 ) )   d y

2 - 1 4 y 4 0 1 + 1 2 y 2 0 1

M = 1 2

Para M x :

M x = ∫ 0 1 ∫ y 2 2 - y 2 y y + 1 d x   d y

∫ 0 1 ( y y + 1 x y 2 2 y - y 2 d y

∫ 0 1 2 y - y 3 + y d y

2 - 1 5 y 5 0 1 + 1 3 y 3 0 1

M x = 4 15

Para M y :

M y =   ∫ 0 1 ∫ y 2 2 y - y 2 x y + 1 d x   d y

∫ 0 1 y + 1 2 x 2 y 2 2 y - y 2 d y

∫ 0 1 - 2 y 4 + 2 y 2 d y  

- 2 5 y 5 0 1 + 2 3 y 3 0 1

M y = 4 15

Logo temos que:

x c . m = y c . m = 4 15 1 2 = 8 15

Passo 3

Para I x :

I x = ∫ 0 1 ∫ y 2 2 y - y 2 y 2 y + 1 d x   d y

∫ 0 1 ( y 2 y + 1 x y 2 2 y - y 2 d y

∫ 0 1 2 y 2 y - y 3   d y

1 2 x 4 0 1 - 1 3 x 6 0 1

I x = 1 6

Resposta

x c . m = y c . m = 8 15

I x = 1 6

Exercícios de Livros Relacionados

Um sólido tem a forma de um cilindro circular reto de raio de base a e altura h . Determinar o momento de inércia do sólido em relação ao eixo de simetria, se a densidade no ponto P é proporcional à d
Calcular a massa e o centro de massa do sólido delimitado por y = x 2 ,y = 9 ,z = 0ey + z = 9 , considerando a densidade de massa igual a x k g / m 3 .
Determine o centro de massa de uma semi-esfera, cuja densidade no ponto P é proporcional à distância de P ao centro.
Calcule o centro de massa da Semi-esfera homogênia x 2 + y 2 + z 2 ≤ R 2 e z ≥ 0( R0 ) .
Sabendo que a densidade em cada ponto de um sólido W é dada por f x ,y ,z = 1 x 2 + y 2 + z 2 , determine a massa de W quando W = x ,y ,z ∈ R 3|x 2 + y 2 + z 2 ≤ 9ex 2 + y 2 + z 2 ≥ 2 y