Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 42
Encontre Compare os gráficos de e e use-os para explicar por que sua resposta é razoável.
Passo 1
Opa, vamos fazer essa questão! O enunciado nos dá:
Pede pra a gente calcular sua derivada e plotar os gráficos de e pra vermos se o calculado é coerente!
Bora lá?!
Passo 2
A nossa função é:
Vamos derivar a função pela regra de derivação da potência que é:
A nossa então fica:
Passo 3
Agora a gente esboça o gráfico das duas funções.
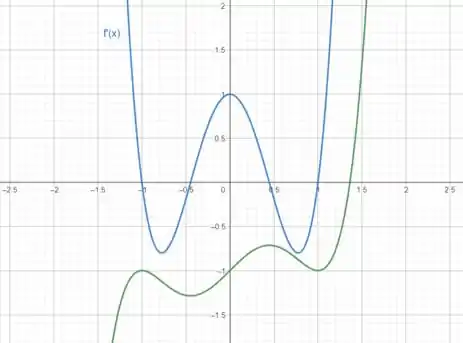
Agora vamos analisar!
Veja que quando é crescente, é positiva e quando é decrescente, e negativa e justamente onde passa de crescente pra decrescente (e vice e versa) é justamente o ponto onde ’.
Portanto, nossa derivada está justificada!
Resposta
Exercícios de Livros Relacionados
Encontre d y d x usando o método da derivação logarítimica: y = x s e n( x )
Encontre d y d x : y = e x l n ( x )
Encontre d y d x usando o método da derivação logarítimica: y = ( ln ( x ) ) t g ( x )
Encontre d y d x usando o método da derivação logarítimica: y = ln ( x ) l n ( x )
Encontre d y d x usando o método da derivação logarítimica: y = x 3 - 2 x l n ( x )