Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.3 - Ex. 76
Suponha que a população de bactérias aeróbicas em um pequeno lago seja modelada pela equação
Onde é a população (em bilhões) dias depois da observação inicial no tempo .
(a) Use um recurso computacional para fazer o gráfico da função
(b) Descreva o que acontececom a população no decorrer do tempo. Verifique sua conclusão encontrando .
(c) Descreva o que acontece com a taxa de crescimento populacional no decorrer do tempo. Verifique sua conclusão fazendo o gráfico de .
Passo 1
(a)
Usando recursos computacionais chegamos no seguinte gráfico:
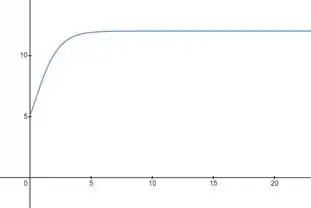
É importante lembrar que não faz tanto sentido pegar a parte do gráfico aonde , pois é uma quantidade de dias e a observação inicial acontece em
Passo 2
(b)
Com a população depende do ar, elas devem crescer até tender a um certo valor limite.
Olhando para o gráfico conseguimos perceber que a população de bactérias aeróbicas ao longo do tempo aumenta, com tendência de chegar a um valor um pouco acima de 10 bilhões para um período de dias muito longo.
Para
Então:
De fato, para períodos muito grandes de tempo população de bactérias aeróbicas tende a
Passo 3
(c)
Quanto mais bactérias aeróbicas, menor a quantidade de oxigênio disponível para o crescimento de mais bactérias. Ou seja, pra períodos muito grandes essa taxa de crescimento tende a diminuir e ir a zero.
Achando
Usando a regra da derivação da divisão:
Se obtivermos o gráfico de :
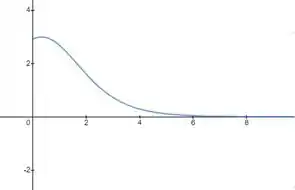
De fato, para períodos de tempo muito longos a taxa de crescimento tende a zero.
Resposta
Ei, a resposta está no passo a passo :)