Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.1 - Ex. 20
Encontre o comprimento de arco da curva do ponto P ao ponto Q.
Passo 1
Bom galera, antes de começar vamos lembrar isolar o x, para sabermos qual a função vamos trabalhar.
Como fazemos isso? Tirando a raiz, não é?
Então podemos chamar:
Como se calcula o comprimento de um arco? Basta lembrarmos que:
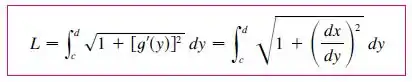
Precisamos da derivada da função g. Como temos uma função “dentro” de outra, usamos a Regra da Cadeia:
E quanto aos intervalos? Vamos pensar !
A nossa variável y vai de 5, no ponto P, até 8, no ponto Q. Então:
Vamos tirar o MMC:
Passo 2
Já descobrimos a integral. Agora vamos resolvê-la. Como?
Vamos usar a substituição:
Derivando:
Substituímos:
Resolvendo:
Substituímos nosso u:
Agora sim, vamos aplicar o intervalo:
Resposta
Exercícios de Livros Relacionados
23- Comprimento de um segmento de reta Use a fórmula de comprimento de arco (Equação 3) para determinar o comprimento do segmento de reta y = 3 - 2 x , 0 ≤ x ≤ 2 . Verifique sua resposta determinando
Nos Exercícios 1-10, determine o con1primento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são.4- x = y 3 2 3 - y 1 2d e y = 1ay = 9
24- Circunferência de um círculo Estabeleça uma integral para determinar a circunferência de um círculo de raio r centrado na origem. Você aprenderá a calcular a integral na Seção 8.3
29- Aproxime o comprimento do arco de um quarto de círculo unitário ( que é π / 2 ) pelo cálculo do comprimento da aproximação poligonal com n = 4 segmentos (veja a figura a seguir).
Determine os comprimentos das curvas nos Exercícios 17-20.19. y = x 2 - ln x / 8 , 1 ≤ x ≤ 2