Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.9 - Ex. 3e
Encontre a curvatura e o raio de curvatura no ponto dado. Trace um esboço da curva e o círculo de curvatura.
;
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Pra começarmos esse exercício, precisamos lembrar do conceito de curvatura e do raio de curvatura. Na seção do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., o Teorema (página ) dessa seção nos dá uma fórmula mais fácil para o cálculo da curvatura de uma curva e é dada por:
Tal que:
é o vetor velocidade;
é a velocidade escalar;
é o vetor aceleração.
Essas definições se encontram na Seção no item Definição do livro.
Para resolver o numerador, precisamos nos recordar que o produto vetorial entre dois vetores pode ser resolvido através do determinante. Supondo dois vetores e , o produto vetorial entre eles é:
Além disso, considerando ainda um ponto , o raio de curvatura é dado como o inverso da curvatura, ou seja:
nas funções curvatura e raio de curvatura. Mas como determinar essa variável? É bem simples: temos que o vetor possui duas coordenadas e na forma , assim como o ponto dado. Então, basta igualar as coordenadas do vetor com a sua respectiva coordenada do ponto. Para esse exercício, temos:
Logo:
O único valor de que atende a nossa equação é
Isso também pode ser verificado pelos elementos do vetor e do ponto.
Passo 2
Dessa forma, para calcularmos a curvatura através da fórmula dada, precisamos determinar a primeira e segunda derivada. Então, derivando-a, teremos:
Tal que:
Ou seja:
Derivando novamente:
A partir da equação da curvatura dada, temos que:
Resolvendo o produto vetorial pelo determinante:
Então:
Esse resultado pode ser denotado como o vetor:
Assim:
Passo 3
Calculando o módulo do vetor do numerador:
Agora, substituindo o valor de :
Isso resulta em:
Passo 4
Com o valor da curvatura determinado, sabemos qual é o raio de curvatura. Então:
Logo:
Passo 5
Para encontrarmos a equação da curva, podemos fazer o seguinte: usar os componentes e de e fazer uma manipulação algébrica para determinar uma equação em função dessas componentes. Dessa forma, teremos:
e
Somando essas duas equações, obtemos:
Isolando a função exponencial:
Aplicando o logaritmo neperiano:
E a propriedade que diz:
Conseguimos:
Agora, lembrando das identidades trigonométricas:
E:
As variáveis podem ser reescritas como:
E:
Aplicando a razão :
Por fim, substituindo o valor de e isolando :
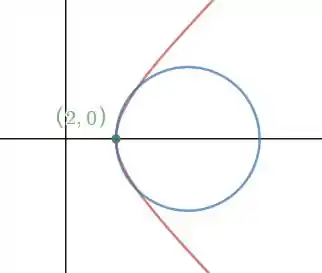
Então, esboçando a curva (em vermelho) e o círculo de curvatura (em azul), iremos obter:
