Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.9 - Ex. 3b
Encontre a curvatura e o raio de curvatura no ponto dado. Trace um esboço da curva e o círculo de curvatura.
;
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Pra começarmos esse exercício, precisamos lembrar do conceito de curvatura e do raio de curvatura. Na seção do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., temos que a curvatura de uma curva é a medida da taxa de variação de sua direção e pode ser dada por:
Quando a curva é plana e possui a forma cartesiana .
Considerando ainda um ponto , o raio de curvatura é dado como o inverso da curvatura, ou seja:
Passo 2
Dessa forma, para calcularmos a curvatura através da fórmula dada, precisamos determinar a primeira e segunda derivada da função dada. Então, derivando-a uma vez, teremos:
E, fazendo isso novamente:
Com esses dois resultados, conseguimos encontrar a forma da curvatura substituindo-as na sua fórmula dada no Passo anterior. Logo, a curvatura pode ser calculada como:
Tal que:
Podemos juntar os termos que possuem o mesmo expoente:
Que resulta em:
Para sabermos o valor da curvatura no ponto dado precisamos substituir a coordenada dele nessa última equação, ou seja:
Portanto:
Passo 3
Com o valor da curvatura determinado, sabemos qual é o raio de curvatura. Então:
Logo:
Passo 4
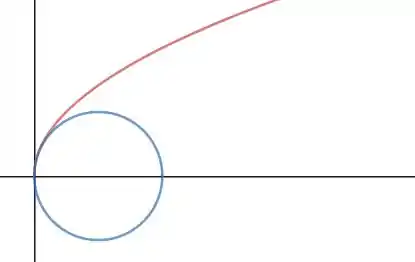
Com o software online Desmos, podemos esboçar a curva (em vermelho) e o círculo de curvatura (em azul), e obter:
