Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 19

19 - Encontre a derivada direcional de f x , y = x y no ponto P ( 2,8 ) na direção do ponto Q ( 5,4 ) .

Passo 1

E aí, galera! Tudo bem?

Nessa questão nós temos a função f x , y = x y e queremos obter a derivada dela no ponto 2,8 e na direção do ponto 5,4 .

A derivada de uma função f na direção de um vetor unitário u é dada por:

D u f = ∇ f ⋅ u

Portanto, para determinar D u f nós precisamos encontrar o gradiente da função f e depois fazer o produto escalar com o vetor u .

Vamos às contas.

Passo 2

Primeiramente, encontraremos as derivadas parciais das coordenadas da equação, com isso poderemos encontrar o vetor gradiente que será dado pela fórmula:

∇ f x , y =   f x , f y  

Descobrindo nosso gradiente:

Derivando a função f x ,   y ,   z = x y       com relação a x , obtemos:

∂ f ∂ x = ∂ ∂ x x y  

∂ f ∂ x = 1 2 x y y

Agora a derivando com relação a y :

∂ f ∂ y = ∂ ∂ y x y  

∂ f ∂ y = 1 2 x y x

Dessa forma, o gradiente se escreve como:

∇ f = y 2 x y , x 2 x y  

Desse modo, o gradiente no ponto 2,8 é:

∇ f ( 2,8 ) = 8 2 2 ⋅ 8 , 2 2 2 ⋅ 8  

∇ f ( 2,8 ) = 8 2 ⋅ 4 , 2 2 ⋅ 4  

∇ f ( 2,8 ) = 1 , 1 4  

Passo 3

O vetor unitário u ^ que dá a direção da derivada pode ser encontrado da seguinte forma. Primeiro vamos ver o vetor que dá a direção do ponto Q 5,4 com relação ao ponto P ( 2,8 ) .   Veja na figura abaixo:

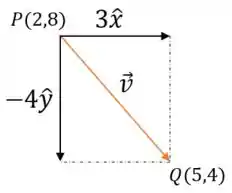
Note que esse vetor não é unitário, pois tem módulo

v = 3 2 + - 4 2   = 5

O vetor unitário u na direção de v é basicamente o vetor v dividido pelo seu módulo, isto é,

u = v v = 3 5 , - 4 5

Passo 4

Sendo assim, nossa derivada direcional no ponto ( 2,8 ) será:

D u f 2,8 = ∇ f 2,8 ⋅ u

D u f 2,8 =   1 , 1 4   ⋅ 3 5 , - 4 5

Realizando esse produto escalar, temos

D u f 2,8 = 3 5 - 1 5 = 2 5

Resposta

D u f 2,8   = 2 /   5  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. O Capitão Astro está outra vez em perigo perto da orbita de Mercúrio. Ele está na posição P 0 = ( 1,1 , 1 ) , e a temperatura de blindagem de sua espaçonave num ponto ( x , y , z ) é dada por T x
O mapa de contorno mostra a temperatura máxima média em novembro de 2004 (em ºC). Estime o valor da derivada direcional da função da temperatura em Dubbo, New South Wales, na direção de Sydney. Quais
Retas no plano xy Mostre que A(x – x0) + B(y – y0) = 0 é uma equação para a reta no plano xy passando pelo ponto (x0, y0) normal ao vetor N = Ai + Bj.
Retas no plano xy Mostre que A(x – x0) + B(y – y0) = 0 é uma equação para a reta no plano xy passando pelo ponto (x0, y0) normal ao vetor N = Ai + Bj.