Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.8 - Ex. 2
a) Use uma calculadora gráfica ou um computador para traçar o círculo . Na mesma tela, trace diversas curvas da forma até que você encontre duas que apenas toquem o círculo. Qual o significado dos valores de dessas duas curvas?
b) Utilize os multiplicadores de Lagrange para determinar os valores extremos de sujeita à restrição . Compare sua resposta com a da parte (a).
Passo 1
Opa!! Tudo tranquilinho?? Bom... nessa questãozinha primeiramente queremos plotar a circunferência dada por:
E, na mesma plotagem, vamos traçar várias curvas com o seguinte formato:
Onde é uma constante.
O nosso objetivo nessa parte é entender o significado de .
Em seguida, o enunciado nos deu essa funçãozinha:
Queremos determinar os valores máximo e mínimo da função sujeita a seguinte restrição:
Para determinarmos os valores, teremos que utilizar o Método dos Multiplicadores de Lagrange!!
Mas que método é esse???
Então... para determinar os valores máximo e mínimo de sujeitos à restrição (supondo que esses valores extremos existam e que sobre a superfície ), então:
Esse é o nosso multiplicador de Lagrange!!!
Se ainda ficou confuso, é o seguinte: Primeiro vamos calcular os gradientes de (ou seja, ) e depois os de (ou seja, ).
Em seguida iremos calcular o valor de utilizando a equação que você acabou de ver. Com isso, aplicando na nossa restrição encontraremos os valores de máximo e mínimo!!!
Feito isso, vamos comparar o resultado com o que a gente descobriu anteriormente sobre .
Agora bora lá!! 😉
Passo 2
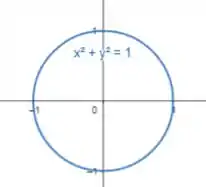
Bom... primeiramente vamos plotar a circunferência :
Agora vamos selecionar alguns valores de e plotar seu gráfico em seguida:
- Para , temos:
- Para , temos:
- Para , temos:
Plotando essas funções junto com a circunferência que plotamos anteriormente, teremos:
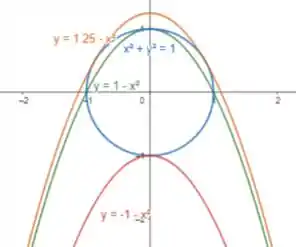
Note que esses valores de parecem dar curvas que são tangentes ao círculo.
Dessa forma, podemos perceber que esses valores representam possíveis valores extremos da função!!
Agora vamos para a segunda parte da nossa questão!!
Passo 3
Vamos então tirar os gradientes das nossas funções!
Primeiro vamos para a função :
Para calcular o gradiente , basta aplicarmos as derivadas parciais!!
Derivando em relação a aplicando a Regra da Potência, temos:
Derivando em relação a :
Assim, nosso gradiente é:
Passo 4
Agora vamos para a função :
Derivando com relação a , obtemos:
Derivando em relação a :
Assim, nosso gradiente é:
Passo 5
Beleza, temos nossos gradientes, agora vamos encontrar um que satisfaça a equação.
Para isso, basta aplicarmos os gradientes que encontramos no passo anterior na equação que apresentamos no Passo 1:
Daí, vamos tirar que:
Da primeira equação, temos:
Daqui podemos perceber dois possíveis resultados: Ou ou .
Vamos analisar cada caso?? 😉
Passo 6
Primeiro vamos analisar o que acontece quando .
Substituindo esse valor na segunda equação do sistema, obtemos:
E, com isso, aplicando esse valor na nossa restrição , obtemos:
Passo 7
Agora, analisando o caso em que , ao aplicar na equação da nossa restrição, obteremos:
Assim, de acordo com os Passos e , temos os possíveis pontos extremos:
E
Agora vamos aplicar eles em !!
Passo 8
Aplicando o ponto em , obteremos:
Aplicando o ponto em , teremos:
E, aplicando o ponto em , teremos:
Com isso, podemos concluir que teremos o ponto de máximo em:
E ponto de mínimo em:
Exatamente o que vimos na primeira parte da questão!! 😉
Prontinho! Conseguimos!
Resposta
(a)
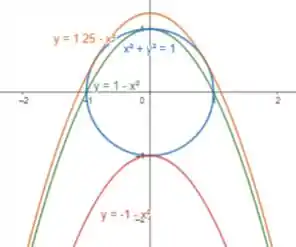
Os valores representam possíveis valores extremos da função.
(b)
Ponto de máximo em:
E ponto de mínimo em: